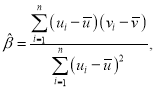题目内容
【题目】如图,椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,
,![]() ,且
,且![]() ,
,![]() 为等边三角形,过点
为等边三角形,过点![]() 的直线与椭圆
的直线与椭圆![]() 在
在![]() 轴右侧的部分交于
轴右侧的部分交于![]() 、
、![]() 两点.
两点.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)求四边形![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() ;(2)
;(2) .
.
【解析】
(1)根据![]() 坐标和
坐标和![]() 为等边三角形可得
为等边三角形可得![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)①当直线![]() 斜率不存在时,易求
斜率不存在时,易求![]() 坐标,从而得到所求面积;②当直线
坐标,从而得到所求面积;②当直线![]() 的斜率存在时,设方程为
的斜率存在时,设方程为![]() ,与椭圆方程联立得到韦达定理的形式,并确定
,与椭圆方程联立得到韦达定理的形式,并确定![]() 的取值范围;利用
的取值范围;利用![]() ,代入韦达定理的结论可求得
,代入韦达定理的结论可求得![]() 关于
关于![]() 的表达式,采用换元法将问题转化为
的表达式,采用换元法将问题转化为 ,
,![]() 的值域的求解问题,结合函数单调性可求得值域;结合两种情况的结论可得最终结果.
的值域的求解问题,结合函数单调性可求得值域;结合两种情况的结论可得最终结果.
(1)![]() ,
,![]() ,
,
![]() 为等边三角形,
为等边三角形,![]() ,
,![]() 椭圆的标准方程为
椭圆的标准方程为![]() .
.
(2)设四边形![]() 的面积为
的面积为![]() .
.
①当直线![]() 的斜率不存在时,可得
的斜率不存在时,可得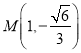 ,
, ,
,
 .
.
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
设![]() ,
,![]() ,
,
联立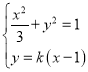 得:
得:![]() ,
,
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
面积![]()

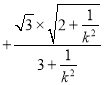 .
.
令![]() ,则
,则![]() ,
,![]() ,
,
令![]() ,则
,则![]()
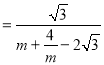 ,
,![]() ,
,
![]()
![]() 在定义域内单调递减,
在定义域内单调递减,![]() .
.
综上所述:四边形![]() 面积的取值范围是
面积的取值范围是 .
.

练习册系列答案
相关题目