题目内容
【题目】线段AB为圆![]() 的一条直径,其端点A,B在抛物线
的一条直径,其端点A,B在抛物线![]() 上,且A,B两点到抛物线C焦点的距离之和为11.
上,且A,B两点到抛物线C焦点的距离之和为11.
(1)求抛物线C的方程及直径AB所在的直线方程;
(2)过M点的直线l交抛物线C于P,Q两点,抛物线C在P,Q处的切线相交于N点,求![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用抛物线的定义可求出![]() ,再利用点差法求出直线
,再利用点差法求出直线![]() 的斜率,结合直线
的斜率,结合直线![]() 过圆心
过圆心![]() ,利用点斜式即可求出直线
,利用点斜式即可求出直线![]() 的方程:
的方程:
(2)不妨设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,与抛物线方程联立,利用韦达定理和弦长公式可求出
,与抛物线方程联立,利用韦达定理和弦长公式可求出![]() ,再利用导数的几何意义求出抛物线
,再利用导数的几何意义求出抛物线![]() 在
在![]() ,
,![]() 的切线方程,把点
的切线方程,把点![]() ,
,![]() 代入切线
代入切线![]() 的方程得
的方程得![]() ,同理可得:
,同理可得:![]() ,故
,故![]() ,
,![]() 为一元二次方程
为一元二次方程![]() 的两根,再次利用韦达定理得
的两根,再次利用韦达定理得![]() ,
,![]() ,所以点
,所以点![]() 到直线
到直线![]() 的距离
的距离![]() ,所以
,所以![]() ,故当
,故当![]() 时,
时,![]() 的面积取得最小值,最小值为27.
的面积取得最小值,最小值为27.
解:(1)设![]()
![]() ,抛物线的焦点为F,
,抛物线的焦点为F,
则![]() ,
,
又![]()
![]()
![]() ,
,
![]() 抛物线C的方程为:
抛物线C的方程为:![]() ,
,
由 ,两式相减得:
,两式相减得:![]() ,
,
![]() 直线AB的斜率为﹣1,
直线AB的斜率为﹣1,
圆M方程:![]() 化为坐标方程为:
化为坐标方程为:
![]() ,
,
![]() 直线AB过圆心
直线AB过圆心![]() ,
,
![]() 直线AB的方程为:
直线AB的方程为:![]() ,即
,即![]() ;
;
(2)不妨设![]()
![]()
![]() ,
,
直线l的方程为![]() ,
,
联立方程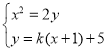 ,消去y得:
,消去y得:![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() 抛物线C的方程为
抛物线C的方程为![]() ,
,
![]()
![]() ,
,
![]() 抛物线C在
抛物线C在![]() 的切线方程为:
的切线方程为:![]() ,
,
又![]() 点
点![]() 在切线PN上,
在切线PN上,
则![]() ,即
,即![]() ,
,
同理可得:![]() ,
,
故![]()
![]() 为一元二次方程
为一元二次方程![]() 的两根,
的两根,
![]()
![]() ,又
,又![]()
![]() ,
,
![]()
![]() ,
,
![]() 点N到直线PQ的距离
点N到直线PQ的距离
 ,
,
![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() 的面积取得最小值,最小值为27,
的面积取得最小值,最小值为27,
![]() 面积的取值范围为:
面积的取值范围为:![]() .
.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】2018年3月5日上午,李克强总理做政府工作报告时表示,将新能源汽车车辆购置税优惠政策再延长三年,自2018年1月1日至2020年12月31日,对购置的新能源汽车免征车辆购置税.新能源汽车销售的春天来了!从衡阳地区某品牌新能源汽车销售公司了解到,为了帮助品牌迅速占领市场,他们采取了保证公司正常运营的前提下实行薄利多销的营销策略(即销售单价随日销量![]() (台)变化而有所变化),该公司的日盈利
(台)变化而有所变化),该公司的日盈利![]() (万元),经过一段时间的销售得到
(万元),经过一段时间的销售得到![]() ,
,![]() 的一组统计数据如下表:
的一组统计数据如下表:
日销量 | 1 | 2 | 3 | 4 | 5 |
日盈利 | 6 | 13 | 17 | 20 | 22 |
将上述数据制成散点图如图所示:
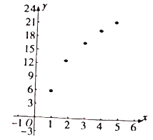
(1)根据散点图判断![]() 与
与![]() 中,哪个模型更适合刻画
中,哪个模型更适合刻画![]() ,
,![]() 之间的关系?并从函数增长趋势方面给出简单的理由;
之间的关系?并从函数增长趋势方面给出简单的理由;
(2)根据你的判断及下面的数据和公式,求出![]() 关于
关于![]() 的回归方程,并预测当日销量
的回归方程,并预测当日销量![]() 时,日盈利是多少?
时,日盈利是多少?
参考公式及数据:线性回归方程![]() ,其中
,其中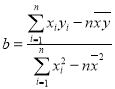 ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
【题目】中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷(guǐ)影长的记录中,冬至和夏至的晷影长是实测得到的,其它节气的晷影长则是按照等差数列的规律计算得出的.下表为《周髀算经》对二十四节气晷影长的记录,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸=10分).
分(1寸=10分).
节气 | 冬至 | 小寒 (大雪) | 大寒 (小雪) | 立春 (立冬) | 雨水 (霜降) | 惊蛰 (寒露) | 春分 (秋分) | 清明 (白露) | 谷雨 (处暑) | 立夏 (立秋) | 小满 (大暑) | 芒种 (小暑) | 夏至 |
晷影长 (寸 | 135 |
|
|
|
|
| 75.5 |
|
|
|
|
| 16.0 |
已知《易经》中记录某年的冬至晷影长为130.0寸,夏至晷影长为14.8寸,按照上述规律那么《易经》中所记录的春分的晷影长应为( )
A.91.6寸B.82.0寸C.81.4寸D.72.4寸
