题目内容
7．
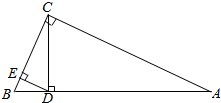如图所示，在△ABC中，∠ACB=90°，CD⊥AB于点D，DE⊥BC于E，若AD=$\frac{3}{2}$$\sqrt{10}$，BE=2．求BC的长．
分析 设BC=x，BD=y，利用射影定理，建立方程，即可求BC的长．
解答 解：设BC=x，BD=y，则
∵在△ABC中，∠ACB=90°，CD⊥AB于点D，DE⊥BC于E，
∴BC2=BD•BA，BD2=BE•BC，
∵AD=$\frac{3}{2}$$\sqrt{10}$，BE=2，
∴x2=y•（y+$\frac{3}{2}$$\sqrt{10}$），y2=2x，
联立解得x=5，y=$\sqrt{10}$，
∴BC=5．
点评 本题考查射影定理，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
17．已知F1，F2分别是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）左、右焦点，P是双曲线右支上一点，若以F2圆心，半径为a的圆与直线PF1相切于P，则双曲线的渐近线为（ ）
| A． | y=±$\frac{\sqrt{6}}{3}$x | B． | y=±$\frac{\sqrt{10}}{2}$x | C． | y=±$\frac{\sqrt{10}}{5}$x | D． | y=±$\frac{\sqrt{6}}{2}$x |
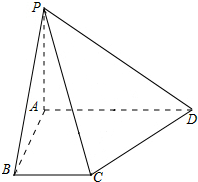如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，BC∥AD，且PA=AB=1，CD=$\sqrt{2}$，AD=2．
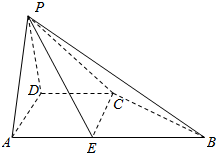在四棱锥P-ABCD中，PD⊥底面ABCD，AB∥CD，PD=CD=AD=$\frac{1}{2}$AB，∠ADC=120°
如图，PD⊥平面ABCD，AD⊥DC，AD∥BC，PD：DC：BC=1：1：$\sqrt{2}$．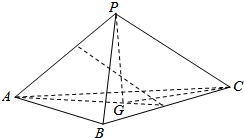
三棱锥P-ABC中，AB=AC=2$\sqrt{10}$，BC=4，PC=点2$\sqrt{11}$，P在平面ABC内的射影恰为△ABC的重心G（即△ABC三条中线的交点）．