题目内容
19.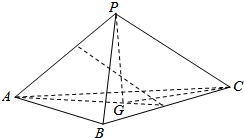 三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=点2$\sqrt{11}$,P在平面ABC内的射影恰为△ABC的重心G(即△ABC三条中线的交点).
三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=点2$\sqrt{11}$,P在平面ABC内的射影恰为△ABC的重心G(即△ABC三条中线的交点).(1)求证:BC⊥平面PAG;
(2)求二面角B-AP-G大小的正切值.
分析 (1)取BC中点D,连接AD、PD,由已知条件推导出PG⊥BC,AG⊥BC,由此能证明BC⊥平面PAG.
(2)以过G作BC的平行线为x轴,AG为y轴,GP为z轴,建立空间直角坐标系,利用向量法能求出二面角B-AP-G大小的正切值.
解答 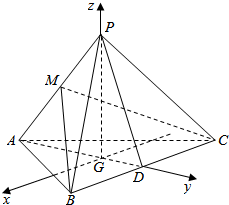 (1)证明:取BC中点D,连接AD、PD,
(1)证明:取BC中点D,连接AD、PD,
∵PG⊥平面ABC,∴PG⊥BC,
等腰△ABC中,G为重心,∴AG⊥BC,
∴BC⊥平面PAG.
(2)△ABC中,AD=6,∴GD=2,
∵BC⊥平面PAG,∴CD⊥PD,
∴PD=2$\sqrt{10}$,∴GP=6,
过G作BC的平行线为x轴,AG为y轴,GP为z轴,
建立空间直角坐标系,
由题意知B(2,2,0),C(-2,2,0),P(0,0,6),A(0,-4,0),
∴M(0,-2,3),
$\overrightarrow{AB}$=(2,6,0),$\overrightarrow{AP}$=(0,4,6),
设平面APB的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=2x+6y=0}\\{\overrightarrow{n}•\overrightarrow{AP}=4y+6z=0}\end{array}\right.$,取x=9,得$\overrightarrow{n}$=(9,-3,2),
又平面APG的法向量$\overrightarrow{m}$=(1,0,0),
设二面角B-AP-G的平面角为θ,
cosθ=|cos<$\overrightarrow{n},\overrightarrow{m}$>|=|$\frac{\overrightarrow{n}•\overrightarrow{m}}{|\overrightarrow{n}|•|\overrightarrow{m}|}$|=$\frac{9}{\sqrt{94}}$,
∴tanθ=$\frac{\sqrt{13}}{9}$,
∴二面角B-AP-G大小的正切值为$\frac{\sqrt{13}}{9}$.
点评 本题考查直线与平面垂直的证明,考查二面角的正切值的求法,解题时要认真审题,注意向量法的合理运用,是中档题.


| A. | 8π | B. | 16π | C. | $\frac{8π}{3}$ | D. | $\frac{16π}{3}$ |
 如图,平面AEFD⊥平面BCFE,其中AEFD为正方形,BCFE为直角梯形,BE∥CF,BE⊥EF,BE=EF=$\frac{1}{2}$CF=1.
如图,平面AEFD⊥平面BCFE,其中AEFD为正方形,BCFE为直角梯形,BE∥CF,BE⊥EF,BE=EF=$\frac{1}{2}$CF=1.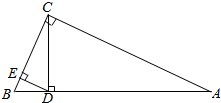 如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥BC于E,若AD=$\frac{3}{2}$$\sqrt{10}$,BE=2.求BC的长.
如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥BC于E,若AD=$\frac{3}{2}$$\sqrt{10}$,BE=2.求BC的长.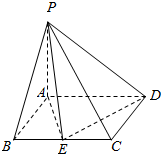 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E为棱BC的中点.
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E为棱BC的中点.