题目内容
17.已知F1,F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)左、右焦点,P是双曲线右支上一点,若以F2圆心,半径为a的圆与直线PF1相切于P,则双曲线的渐近线为( )| A. | y=±$\frac{\sqrt{6}}{3}$x | B. | y=±$\frac{\sqrt{10}}{2}$x | C. | y=±$\frac{\sqrt{10}}{5}$x | D. | y=±$\frac{\sqrt{6}}{2}$x |
分析 由题意,PF1⊥PF2,|PF2|=a,|PF1|=3a,利用勾股定理,即可得出结论.
解答 解:由题意,PF1⊥PF2,|PF2|=a,|PF1|=3a,
∴9a2+a2=4c2,
∴10a2=4(a2+b2),
∴$\frac{b}{a}$=$\frac{\sqrt{6}}{2}$,
∴双曲线的渐近线为y=±$\frac{\sqrt{6}}{2}$x,
故选:D.
点评 本题考查双曲线的定义,直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
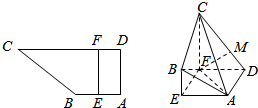 如图所示,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=2,点E在边AB上,点F在边CD上,且EF∥AD,沿EF将面EBCF折起,使得CF⊥AE.
如图所示,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=2,点E在边AB上,点F在边CD上,且EF∥AD,沿EF将面EBCF折起,使得CF⊥AE.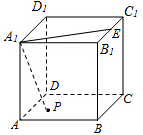 如图,正方体ABCD-A1B1C1D1中,E是棱B1C1的中点,动点P为正方体各面上的任一点.
如图,正方体ABCD-A1B1C1D1中,E是棱B1C1的中点,动点P为正方体各面上的任一点.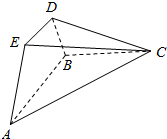 已知△ABC为直角三角形,AB⊥BC,四边形ABDE为等腰梯形,DE∥AB,平面ABDE⊥平面ABC,AB=BC=2DE=2.
已知△ABC为直角三角形,AB⊥BC,四边形ABDE为等腰梯形,DE∥AB,平面ABDE⊥平面ABC,AB=BC=2DE=2. 如图,平面AEFD⊥平面BCFE,其中AEFD为正方形,BCFE为直角梯形,BE∥CF,BE⊥EF,BE=EF=$\frac{1}{2}$CF=1.
如图,平面AEFD⊥平面BCFE,其中AEFD为正方形,BCFE为直角梯形,BE∥CF,BE⊥EF,BE=EF=$\frac{1}{2}$CF=1.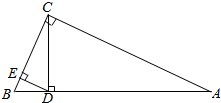 如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥BC于E,若AD=$\frac{3}{2}$$\sqrt{10}$,BE=2.求BC的长.
如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥BC于E,若AD=$\frac{3}{2}$$\sqrt{10}$,BE=2.求BC的长.