题目内容
18.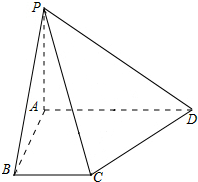 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,且PA=AB=1,CD=$\sqrt{2}$,AD=2.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,BC∥AD,且PA=AB=1,CD=$\sqrt{2}$,AD=2.(1)求四棱锥P-ABCD的体积;
(2)求异面直线PB与CD所成角的大小.
分析 (1)由题意可知棱锥底面为直角梯形,结合已知求出BC,得到底面面积,代入棱锥体积公式得答案;
(2)连接BE,PE,可得∠PBE为异面直线PB与CD所成角,然后通过解直角三角形得答案.
解答 解:(1)如图, 在底面四边形ABCD中,∵AB⊥AD,BC∥AD,
在底面四边形ABCD中,∵AB⊥AD,BC∥AD,
∴四边形ABCD为直角梯形,
过C作CE⊥AD于E,设BC=x,
∵AD=2,AB=1,CD=$\sqrt{2}$,
∴DE=2-x,CE=1,则$(2-x)^{2}+{1}^{2}=(\sqrt{2})^{2}$,
解得:x=1或x=3(舍).
∴BC=1.
又PA=1.
则${V}_{P-ABCD}=\frac{1}{3}×\frac{1}{2}(1+2)×1×1=\frac{1}{2}$;
(2)连接BE,PE,
由BC∥DE,BC=DE,可得四边形BCDE为平行四边形,∴BE∥CD.
则∠PBE为异面直线PB与CD所成角.
在Rt△PAB中,∵PA=AB=1,∴PB=$\sqrt{2}$.
在Rt△PAE中,∵PA=AB=1,∴PE=$\sqrt{2}$.
在△PBE中,由PB=PE=$\sqrt{2}$,BE=$CD=\sqrt{2}$,
∴∠PBE=60°.
点评 本题考查棱柱、棱锥、棱台的体积,考查了异面直线所成的角,考查空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
13.点F(c,0)为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,点P为双曲线左支上一点,线段PF与圆x2+y2=$\frac{{b}^{2}}{4}$相切于点Q,且$\overrightarrow{PQ}$=$\frac{1}{2}$$\overrightarrow{PF}$,则双曲线的离心率等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
3.已知函数f(x)=|x|-1,若关于x的方程f2(x)+(2m-1)f(x)+4-2m=0有四个不同的实数解,则实数m的取值范围是( )
| A. | m<-2 | B. | m<-2.5 | C. | m<1.5 | D. | m>1.5 |
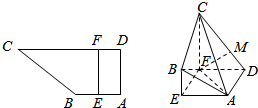 如图所示,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=2,点E在边AB上,点F在边CD上,且EF∥AD,沿EF将面EBCF折起,使得CF⊥AE.
如图所示,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=2,点E在边AB上,点F在边CD上,且EF∥AD,沿EF将面EBCF折起,使得CF⊥AE. 如图,平面AEFD⊥平面BCFE,其中AEFD为正方形,BCFE为直角梯形,BE∥CF,BE⊥EF,BE=EF=$\frac{1}{2}$CF=1.
如图,平面AEFD⊥平面BCFE,其中AEFD为正方形,BCFE为直角梯形,BE∥CF,BE⊥EF,BE=EF=$\frac{1}{2}$CF=1.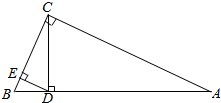 如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥BC于E,若AD=$\frac{3}{2}$$\sqrt{10}$,BE=2.求BC的长.
如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥BC于E,若AD=$\frac{3}{2}$$\sqrt{10}$,BE=2.求BC的长.