题目内容
已知定义在R上的奇函数f(x)满足f(x-4)=-f(x).
(1)求f(2 012)的值;
(2)求证:函数f(x)的图像关于直线x=2对称;
(3)若f(x)在区间[0,2]上是增函数,试比较f(-25),f(11),f(80)的大小.
(1)求f(2 012)的值;
(2)求证:函数f(x)的图像关于直线x=2对称;
(3)若f(x)在区间[0,2]上是增函数,试比较f(-25),f(11),f(80)的大小.
(1)0 (2)见解析 (3) f(-25)<f(80)<f(11)
解:(1)因为f(x-4)=-f(x),
所以f(x)=-f(x-4)=-{-f[(x-4)-4]}=f(x-8),
知函数f(x)的周期为T=8.
所以f(2 012)=f(251×8+4)=f(4)=-f(0).
又f(x)为定义在R上的奇函数.
所以f(0)=0,故f(2 012)=0.
(2)证明:因为f(x)=-f(x-4),
所以f(x+2)=-f[(x+2)-4]=-f(x-2)=f(2-x),
知函数f(x)的图像关于直线x=2对称.
(3)由(1)知f(x)是以8为周期的周期函数,
所以f(-25)=f[(-3)×8-1]=f(-1),
f(11)=f(8+3)=f(3)=-f(-1)=f(1),
f(80)=f(10×8+0)=f(0).
又f(x)在[0,2]上是增函数,且f(x)在R上为奇函数,所以f(x)在[-2,2]上为增函数,则有f(-1)<f(0)<f(1),
即f(-25)<f(80)<f(11).
所以f(x)=-f(x-4)=-{-f[(x-4)-4]}=f(x-8),
知函数f(x)的周期为T=8.
所以f(2 012)=f(251×8+4)=f(4)=-f(0).
又f(x)为定义在R上的奇函数.
所以f(0)=0,故f(2 012)=0.
(2)证明:因为f(x)=-f(x-4),
所以f(x+2)=-f[(x+2)-4]=-f(x-2)=f(2-x),
知函数f(x)的图像关于直线x=2对称.
(3)由(1)知f(x)是以8为周期的周期函数,
所以f(-25)=f[(-3)×8-1]=f(-1),
f(11)=f(8+3)=f(3)=-f(-1)=f(1),
f(80)=f(10×8+0)=f(0).
又f(x)在[0,2]上是增函数,且f(x)在R上为奇函数,所以f(x)在[-2,2]上为增函数,则有f(-1)<f(0)<f(1),
即f(-25)<f(80)<f(11).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
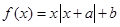 是奇函数的充要条件是
是奇函数的充要条件是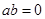
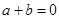
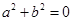
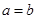
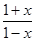
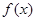 在
在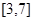 上是增函数且最小值是2,那么
上是增函数且最小值是2,那么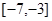 上是( )
上是( )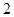
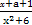 为奇函数,则实数a= .
为奇函数,则实数a= . +2x+m (m为常数),则
+2x+m (m为常数),则 ( )
( )