题目内容
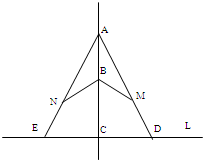
如图,森林的边界是直线L,兔子和狼分别在L的垂线AC上的点A和点B处(AB=BC=a),现兔子沿线AD(或AE)以速度2v准备越过L向森林逃跑,同时狼沿线段BM(点M在AD上)或BN(点N在AE上)以速度v进行追击,若狼比兔子先到或同时到达点M(或N)处,狼就会吃掉兔子.求兔子的所有不幸点(即可能被狼吃掉的地方)组成的区域的面积S.

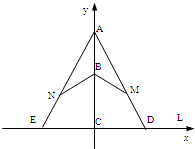
如图所示,建立平面直角坐标系x0y,并设M(x,y).
狼要吃掉兔子需先到达M点或与兔子同时到达M点,即有:
≤
.…(4分)
即2|BM|≤|AM|
∴2
≤
两边平方,整理得:3x2+3y2-4ay≤0
即:x2+(y-
a)2≤(
a)2…(8分)
所以,兔子的所有不幸点构成的区域为圆及其内部.∴S=π•(
a)2=
πa2
所以,兔子的所有不幸点组成的区域的面积S为
πa2.…(10分)
狼要吃掉兔子需先到达M点或与兔子同时到达M点,即有:
| |BM| |
| v |
| |AM| |
| 2v |
即2|BM|≤|AM|
∴2
| x2+(y-a)2 |
| x2+(y-2a)2 |
两边平方,整理得:3x2+3y2-4ay≤0
即:x2+(y-
| 2 |
| 3 |
| 2 |
| 3 |
所以,兔子的所有不幸点构成的区域为圆及其内部.∴S=π•(
| 2 |
| 3 |
| 4 |
| 9 |
所以,兔子的所有不幸点组成的区域的面积S为
| 4 |
| 9 |


练习册系列答案
相关题目



