Question

圆C：x²+y²-2x-2y-7=0，设P是该圆的过点（3，3）的弦的中点，则动点P的轨迹方程是______．

Answer 1

∵圆C：x²+y²-2x-2y-7=0，化成标准方程得（x-1）²+（y-1）²=9，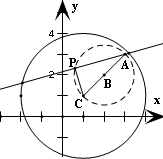
∴圆心为C（1，1），半径r=3．
设A（3，3），连结PC
∵P是该圆的过点（3，3）的弦的中点，
∴PC⊥AP，可得点P在以AC为直径的圆上运动．
∵|AC|=

(3-1)2+(3-1)2

=2

2

，AC的中点为B（2，2）
∴以AC为直径的圆的圆心为B（2，2），半径R=

1

2

|AC|=

2

，
其方程为（x-2）²+（y-2）²=2，即为动点P的轨迹方程．
故答案为：（x-2）²+（y-2）²=2