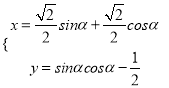题目内容
【题目】已知定义域为![]() 的函数
的函数![]() 存在两个零点.
存在两个零点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,求证:
,求证: ![]() .
.
【答案】(1) ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)分离参数得![]() ,借助函数
,借助函数![]() 的图象进行求解;(2)由于
的图象进行求解;(2)由于![]() ,则
,则![]() 在区间
在区间![]() 上单调递增,
上单调递增, ![]()
![]()
 ,故只需证明
,故只需证明 即可。由题知
即可。由题知![]() 且
且![]() ,不妨设
,不妨设![]() ,则
,则![]() ,构造
,构造![]() ,只需证明
,只需证明![]() 即可,利用导数的知识可求解。
即可,利用导数的知识可求解。
试题解析:
(1)由![]() .得
.得![]() 。
。
令![]() ,则
,则![]() ,
,
当![]() 变化时,
变化时, ![]() 及
及![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
| - | 0 | + |
| 减 | 最小 | 增 |
由表可知,当![]() 时,
时, ![]() 有极小值,也为最小值,且最小值为
有极小值,也为最小值,且最小值为![]() ,
,
当![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() ,
,
∴ ![]()
故![]() 在区间
在区间![]() 上存在两个零点时,
上存在两个零点时, ![]() 的取值范围为
的取值范围为![]() .
.
(2)∵![]() , ∴
, ∴ ![]() ,
,
又![]() ,
,
∴![]()
 ,
,
令![]() ,
,
则 ,
,
由题知![]() 且
且![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
,
∴![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 单调递减,
单调递减,
∴![]() 时,
时, ![]() ,
,
∴ ,
,
又![]() ,
,
∴  ,即
,即![]() ,
,
∴![]() ,
,
∵![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∴![]() ,得证.
,得证.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】为考察高中生的性别与是否喜欢数学课程之间的关系,在我市某普通中学高中生中随机抽取200名学生,得到如下2×2列联表:
喜欢数学课 | 不喜欢数学课 | 合计 | |
男 | 30 | 60 | 90 |
女 | 20 | 90 | 110 |
合计 | 50 | 150 | 200 |
经计算K2≈6.06,根据独立性检验的基本思想,约有(填百分数)的把握认为“性别与喜欢数学课之间有关系”.
【题目】某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高二年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名,现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
分数段 |
|
|
|
|
|
|
男 | 3 | 9 | 18 | 15 | 6 | 9 |
女 | 6 | 4 | 5 | 10 | 13 | 2 |
附表及公式:
| 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
![]()
(1)估计男、女生各自的平均分(同一组数据用该组区间中点值作代表),从计算结果看,数学成绩与性别是否有关;
(2)规定80分以上者为优分(含80分),请你根据已知条件作出 ![]() 列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”.
列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”.