ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋÄģÐĢΊÁËÁË―âĀšĮōÔËķŊĘĮ·ņÓëÐÔąðÏāđØĢŽÔÚļßŌŧÐÂÉúÖÐËæŧúĩũēéÁË40ÃûÄÐÉúšÍ40ÃûÅŪÉúĢŽĩũēéĩÄ―áđûČįÏÂąíĢš
Ïēŧķ | ēŧÏēŧķ | ŨÜžÆ | |
ÅŪÉú | 8 | ||
ÄÐÉú | 20 | ||
ŨÜžÆ |
ĢĻ1ĢĐļųūÝĖâŌâÍęģÉÉÏÃæĩÄÁÐÁŠąíĢŽēĒÓÃķĀÁĒÐÔžėŅéĩÄ·―·Ļ·ÖÎöĢŽÄÜ·ņÔÚ·ļīíĩÄļÅÂĘēŧģŽđý0.01ĩÄĮ°ĖáÏÂČÏΊÏēŧķĀšĮōÔËķŊÓëÐÔąðÓÐđØĢŋ
ĢĻ2ĢĐīÓÅŪÉúÖаīÏēŧķĀšĮōÔËķŊÓë·ņĢŽÓ÷ÖēãģéŅųĩÄ·―·ĻģéČĄ5ČËŨö―øŌŧē―ĩũēéĢŽīÓÕâ5ČËÖÐČÎŅĄ2ČËĢŽĮó2ČËķžÏēŧķĀšĮōÔËķŊĩÄļÅÂĘ.
ļ―Ģš
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
Ąūīð°ļĄŋĢĻ1ĢĐĖîąíĄĒ·ÖÎöžûÏę―âĢŽÄÜÔÚ·ļīíĩÄļÅÂĘēŧģŽđý0.01ĩÄĮ°ĖáÏÂČÏΊÏēŧķĀšĮōÔËķŊÓëÐÔąðÓÐđØĢŧĢĻ2ĢĐ![]() .
.
Ąū―âÎöĄŋ
ĢĻ1ĢĐļųūÝÄÐÉúšÍÅŪÉúļũÓÐ40ļöĢŽžīŋÉĩÃĩ―ąíļņÖÐĩÄËųÓÐĘýūÝĢŽÔŲļųūÝąíļņĘýūÝĢŽĀûÓÃēÎŋžđŦĘ―ĢŽžÆËã![]() ĢŽžīŋÉ―øÐÐÅÐķÏĢŧ
ĢŽžīŋÉ―øÐÐÅÐķÏĢŧ
ĢĻ2ĢĐÏČļųūÝ·ÖēãģéŅųĩÄĩČąČĀýģéČĄĩÄÐÔÖĘĢŽžÆËãģö5ČËÖÐÏēŧķĀšĮōšÍēŧÏēŧķĀšĮōĩÄČËĢŧīÓķøÁÐūŲģöËųÓÐīÓ5ČËÖÐģéČĄ2ČËĩÄŋÉÄÜÐÔĢŽÔŲÕŌģöÂúŨãĖâŌâĩÄŋÉÄÜÐÔĢŽÓÃđÅĩäļÅÐÍļÅÂĘžÆËãđŦĘ―žīŋÉĮóĩÃ.
ĢĻ1ĢĐĖîąíČįÏÂĢš
Ïēŧķ | ēŧÏēŧķ | ŨÜžÆ | |
ÅŪÉú | 32 | 8 | 40 |
ÄÐÉú | 20 | 20 | 40 |
šÏžÆ | 52 | 28 | 80 |
Ąā![]() .
.
ËųŌÔÄÜÔÚ·ļīíĩÄļÅÂĘēŧģŽđý0.01ĩÄĮ°ĖáÏÂČÏΊÏēŧķĀšĮōÔËķŊÓëÐÔąðÓÐđØ.
ĢĻ2ĢĐīÓÅŪÉúÖаīÏēŧķĀšĮōÔËķŊÓë·ņĢŽÓ÷ÖēãģéŅųĩÄ·―·ĻģéČĄ5ČËĢŽ
ÔōÆäÖÐÏēŧķĀšĮōÔËķŊĩÄÓÐ![]() ĢĻČËĢĐĢŽ
ĢĻČËĢĐĢŽ
ēŧÏēŧķĀšĮōÔËķŊĩÄÓÐ![]() ĢĻČËĢĐ
ĢĻČËĢĐ
ÉčÏēŧķĀšĮōÔËķŊĩÄ4ČËžĮΊ![]() ĢŽēŧÏēŧķĀšĮōÔËķŊĩÄžĮΊ
ĢŽēŧÏēŧķĀšĮōÔËķŊĩÄžĮΊ![]() ĢŽ
ĢŽ
ÔōīÓÕâ5ČËÖÐČÎŅĄ2ČËĩÄËųÓÐ―áđûÓÐĢš
![]() ĢŽđē10ÖÖ.
ĢŽđē10ÖÖ.
ÆäÖÐĮĄšÃ2ČËķžÏēŧķĀšĮōÔËķŊĩÄÓÐ![]() ĢŽđē6ÖÖ.
ĢŽđē6ÖÖ.
ËųŌÔīÓÕâ5ČËÖÐČÎŅĄ2ČËĢŽ2ČËķžÏēŧķĀšĮōÔËķŊĩÄļÅÂĘΊ![]() .
.

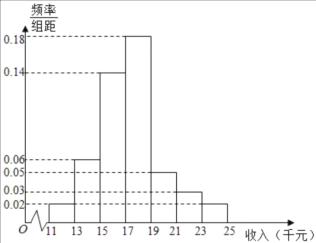
ĄūĖâÄŋĄŋÖÁ2018ÄęĩŨ,ÎŌđú·ĒÃũŨĻĀûÉęĮëÁŋŌŅūÁŽÐø8ÄęÎŧūÓĘĀ―įĘŨÎŧ,ÏÂąíĘĮÎŌđú2012ÄęÖÁ2018Äę·ĒÃũŨĻĀûÉęĮëÁŋŌÔž°ÏāđØĘýūÝ.
ŨÜžÆ | ||||||||
ÄęīúīúÂë | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 28 |
ÉęĮëÁŋ | 65 | 82 | 92 | 110 | 133 | 138 | 154 | 774 |
| 65 | 164 | 276 | 440 | 665 | 828 | 1078 | 3516 |
ŨĒĢšÄęīúīúÂë1~7·ÖąðąíĘū2012~2018.
ĢĻ1ĢĐŋÉŌÔŋīģöÉęĮëÁŋÃŋÄęķžÔÚÔöžÓ,ĮëÎĘÕâžļÄęÖÐÄĮŌŧÄęĩÄÔöģĪÂĘīïĩ―Ũîļß,ŨîļßĘĮķāÉŲĢŋ
ĢĻ2ĢĐ―ĻÁĒ![]() đØÓÚ
đØÓÚ![]() ĩÄŧØđéÖąÏß·―ģĖ(ūŦČ·ĩ―0.01),ēĒÔĪēâÎŌđú·ĒÃũŨĻĀûÉęĮëÁŋÍŧÆÆ200ÍōžþĩÄÄę·Ý.
ĩÄŧØđéÖąÏß·―ģĖ(ūŦČ·ĩ―0.01),ēĒÔĪēâÎŌđú·ĒÃũŨĻĀûÉęĮëÁŋÍŧÆÆ200ÍōžþĩÄÄę·Ý.
ēÎŋžđŦĘ―Ģš .
.
ĄūĖâÄŋĄŋ―üĀīĖėÆøąäŧŊÎÞģĢĢŽķļČŧÉýÎÂĄĒ―ĩηųķČīóÓÚ![]() ĩÄĖėÆøÏÖÏóģöÏÖÔöķā.ķļČŧ―ĩηųķČīóÓÚ
ĩÄĖėÆøÏÖÏóģöÏÖÔöķā.ķļČŧ―ĩηųķČīóÓÚ![]() ČÝŌŨŌýÆðÓŨķųÉË·įļÐðžēēĄ.ΊÁË―âÉË·įļÐðžēēĄĘĮ·ņÓëÐÔąðÓÐđØĢŽÔÚÄģļūÓŨąĢ―ĄÔšËæŧúķÔČËÔšĩÄ
ČÝŌŨŌýÆðÓŨķųÉË·įļÐðžēēĄ.ΊÁË―âÉË·įļÐðžēēĄĘĮ·ņÓëÐÔąðÓÐđØĢŽÔÚÄģļūÓŨąĢ―ĄÔšËæŧúķÔČËÔšĩÄ![]() ÃûÓŨķų―øÐÐĩũēé,ĩÃĩ―ÁËČįÏÂĩÄÁÐÁŠąí,ČôÔÚČŦēŋ
ÃûÓŨķų―øÐÐĩũēé,ĩÃĩ―ÁËČįÏÂĩÄÁÐÁŠąí,ČôÔÚČŦēŋ![]() ÃûÓŨķųÖÐËæŧúģéČĄ
ÃûÓŨķųÖÐËæŧúģéČĄ![]() ČËĢŽģéĩ―ŧžÉË·įļÐðžēēĄĩÄÓŨķųĩÄļÅÂĘΊ
ČËĢŽģéĩ―ŧžÉË·įļÐðžēēĄĩÄÓŨķųĩÄļÅÂĘΊ![]() ,
,
(1)Įë―ŦÏÂÃæĩÄÁÐÁŠąíēđģäÍęÕû;
ŧžÉË·įļÐðžēēĄ | ēŧŧžÉË·įļÐðžēēĄ | šÏžÆ | |
ÄÐ | 25 | ||
ÅŪ | 20 | ||
šÏžÆ | 100 |
(2)ÄÜ·ņÔÚ·ļīíÎóĩÄļÅÂĘēŧģŽđý![]() ĩÄĮéŋöÏÂČÏΊŧžÉË·įļÐðžēēĄÓëÐÔąðÓÐđØ?ËĩÃũÄãĩÄĀíÓÉ;
ĩÄĮéŋöÏÂČÏΊŧžÉË·įļÐðžēēĄÓëÐÔąðÓÐđØ?ËĩÃũÄãĩÄĀíÓÉ;
(3)ŌŅÖŠÔÚŧžÉË·įļÐðžēēĄĩÄ![]() ÃûÅŪÐÔÓŨķųÖÐ,ÓÐ
ÃûÅŪÐÔÓŨķųÖÐ,ÓÐ![]() ÃûÓÖŧžŧÆķŧēĄ.ÏÖÔÚīÓŧžÉË·įļÐðžēēĄĩÄ
ÃûÓÖŧžŧÆķŧēĄ.ÏÖÔÚīÓŧžÉË·įļÐðžēēĄĩÄ![]() ÃûÅŪÐÔÖÐ,ŅĄģö
ÃûÅŪÐÔÖÐ,ŅĄģö![]() Ãû―øÐÐÆäËû·―ÃæĩÄÅÅēé,žĮŅĄģöŧžŧÆķŧēĄĩÄÅŪÐÔČËĘýΊ
Ãû―øÐÐÆäËû·―ÃæĩÄÅÅēé,žĮŅĄģöŧžŧÆķŧēĄĩÄÅŪÐÔČËĘýΊ![]() ,Įó
,Įó![]() ĩÄ·ÖēžÁÐŌÔž°ĘýŅ§ÆÚÍû.ÏÂÃæĩÄÁŲ―įÖĩąíđĐēÎŋž:
ĩÄ·ÖēžÁÐŌÔž°ĘýŅ§ÆÚÍû.ÏÂÃæĩÄÁŲ―įÖĩąíđĐēÎŋž:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ēÎŋžđŦĘ―Ģš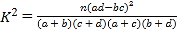 ĢŽÆäÖÐ
ĢŽÆäÖÐ![]()