题目内容
【题目】近来天气变化无常，陡然升温、降温幅度大于
的天气现象出现增多.陡然降温幅度大于容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关，在某妇幼保健院随机对人院的
名幼儿进行调查,得到了如下的列联表,若在全部名幼儿中随机抽取
人，抽到患伤风感冒疾病的幼儿的概率为
,
(1)请将下面的列联表补充完整;
患伤风感冒疾病 | 不患伤风感冒疾病 | 合计 | |
男 | 25 | ||
女 | 20 | ||
合计 | 100 |
(2)能否在犯错误的概率不超过
的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
(3)已知在患伤风感冒疾病的
名女性幼儿中,有
名又患黄痘病.现在从患伤风感冒疾病的名女性中,选出名进行其他方面的排查,记选出患黄痘病的女性人数为
,求的分布列以及数学期望.下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式：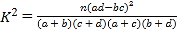
，其中
【答案】(1)见解析,(2) 不能在犯错误的概率不超过
的情况下认为患伤风感冒疾病与性别有美.(3)分布列见解析,
【解析】
(1)根据在全部
名幼儿中随机抽取
人，抽到患伤风感冒疾病的幼儿的概率为
,可以求出患伤风感冒疾病的幼儿的数量，这样可以补充完成列联表；
(2)代入公式求出
的值，根据所给的表写出结论；
(3) 根据题意,
的值可能为
.分别求出相应的概率值，列出分布列，计算出数学期望即可.
(1)列联表补充如下;
患伤风感冒疾病 | 不患伤风感冒疾病 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
计算的观测值为
,
所以不能在犯错误的概率不超过的情况下认为患伤风感冒疾病与性别有美.
(3)根据题意,的值可能为.
则
,
,
故的分布列如下：
|
|
|
|
|
|
|
|
故的数学期望：
.
53随堂测系列答案【题目】在
中，
，
，
分别为内角
，
，
的对边，且满
.
（1）求的大小；
（2）再在①
，②
，③
这三个条件中，选出两个使唯一确定的条件补充在下面的问题中，并解答问题.若________，________，求的面积.
【题目】2018年反映社会现实的电影《我不是药神》引起了很大的轰动，治疗特种病的创新药研发成了当务之急．为此，某药企加大了研发投入，市场上治疗一类慢性病的特效药品
的研发费用
（百万元）和销量
（万盒）的统计数据如下：
研发费用 | 2 | 3 | 6 | 10 | 13 | 15 | 18 | 21 |
销量 | 1 | 1 | 2 | 2.5 | 3.5 | 3.5 | 4.5 | 6 |
（1）求与的相关系数
精确到0.01，并判断与的关系是否可用线性回归方程模型拟合？（规定：
时，可用线性回归方程模型拟合）；
（2）该药企准备生产药品的三类不同的剂型
，
，
，并对其进行两次检测，当第一次检测合格后，才能进行第二次检测．第一次检测时，三类剂型，，合格的概率分别为
，
，
，第二次检测时，三类剂型，，合格的概率分别为，，
．两次检测过程相互独立，设经过两次检测后，，三类剂型合格的种类数为
，求的数学期望．
附：（1）相关系数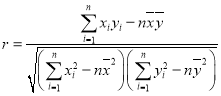
（2）
，
，
，
．
【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数
（个）和温度
（
）的7组观测数据，其散点图如所示：
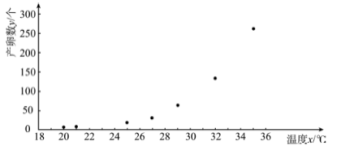
根据散点图，结合函数知识，可以发现产卵数和温度可用方程
来拟合，令
，结合样本数据可知
与温度可用线性回归方程来拟合．根据收集到的数据，计算得到如下值：
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中
，
．
（1）求和温度的回归方程（回归系数结果精确到
）；
（2）求产卵数关于温度的回归方程；若该地区一段时间内的气温在
之间（包括
与
），估计该品种一只昆虫的产卵数的范围.（参考数据：
，
，
，
，
．）
附：对于一组数据
，
，…，
，其回归直线
的斜率和截距的最小二乘估计分别为
．
