题目内容
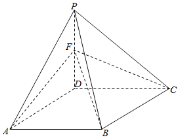
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为边长为2的菱形,∠DAB=60°,∠ADP=90°,面ADP⊥面ABCD,点F为棱PD的中点.
(1)在棱AB上是否存在一点E,使得AF∥面PCE,并说明理由;
(2)当二面角D﹣FC﹣B的余弦值为![]() 时,求直线PB与平面ABCD所成的角.
时,求直线PB与平面ABCD所成的角.
【答案】(1)见解析;(2)45°
【解析】
(1)点E为棱AB的中点取PC的中点Q,连结EQ、FQ,推导出四边形AEQF为平行四边形,从而AF∥EQ,由此能证明AF∥平面PEC.(2)推导出ED⊥CD,PD⊥AD,且从而PD⊥面ABCD,故以D为坐标原点建立空间坐标系,利用向量法能求出直线PB与平面ABCD所成的角.
(1)在棱AB上存在点E,使得AF∥面PCE,点E为棱AB的中点.
理由如下:取PC的中点Q,连结EQ、FQ,由题意,FQ∥DC且![]() ,AE∥CD且
,AE∥CD且![]() ,
,
故AE∥FQ且AE=FQ.所以,四边形AEQF为平行四边形.所以,AF∥EQ,又EQ平面PEC,AF平面PEC,
所以,AF∥平面PEC.
(2)由题意知△ABD为正三角形,所以ED⊥AB,亦即ED⊥CD,又∠ADP=90°,
所以PD⊥AD,且面ADP⊥面ABCD,面ADP∩面ABCD=AD,
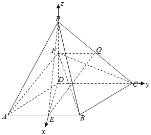
所以PD⊥面ABCD,故以D为坐标原点建立如图空间坐标系,
设FD=a,则由题意知D(0,0,0),F(0,0,a),C(0,2,0),![]() ,
,
![]() ,
,![]() ,设平面FBC的法向量为
,设平面FBC的法向量为![]() ,
,
则由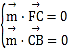 得
得![]() ,令x=1,则
,令x=1,则![]() ,
,![]() ,
,
所以取![]() ,显然可取平面DFC的法向量
,显然可取平面DFC的法向量![]() ,
,
由题意: ,所以a=1.
,所以a=1.
由于PD⊥面ABCD,所以PB在平面ABCD内的射影为BD,
所以∠PBD为直线PB与平面ABCD所成的角,
易知在Rt△PBD中![]() ,从而∠PBD=45°,
,从而∠PBD=45°,
所以直线PB与平面ABCD所成的角为45°.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案【题目】某校为了了解篮球运动是否与性别相关,在高一新生中随机调查了40名男生和40名女生,调查的结果如下表:
喜欢 | 不喜欢 | 总计 | |
女生 | 8 | ||
男生 | 20 | ||
总计 |
(1)根据题意完成上面的列联表,并用独立性检验的方法分析,能否在犯错的概率不超过0.01的前提下认为喜欢篮球运动与性别有关?
(2)从女生中按喜欢篮球运动与否,用分层抽样的方法抽取5人做进一步调查,从这5人中任选2人,求2人都喜欢篮球运动的概率.
附:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
【题目】为了拓展城市的旅游业,实现不同市区间的物资交流,政府决定在![]() 市与
市与![]() 市之间建一条直达公路,中间设有至少8个的偶数个十字路口,记为
市之间建一条直达公路,中间设有至少8个的偶数个十字路口,记为![]() ,现规划在每个路口处种植一颗杨树或者木棉树,且种植每种树木的概率均为
,现规划在每个路口处种植一颗杨树或者木棉树,且种植每种树木的概率均为![]() .
.
(1)现征求两市居民的种植意见,看看哪一种植物更受欢迎,得到的数据如下所示:
A市居民 | B市居民 | |
喜欢杨树 | 300 | 200 |
喜欢木棉树 | 250 | 250 |
是否有![]() 的把握认为喜欢树木的种类与居民所在的城市具有相关性;
的把握认为喜欢树木的种类与居民所在的城市具有相关性;
(2)若从所有的路口中随机抽取4个路口,恰有![]() 个路口种植杨树,求
个路口种植杨树,求![]() 的分布列以及数学期望;
的分布列以及数学期望;
(3)在所有的路口种植完成后,选取3个种植同一种树的路口,记总的选取方法数为![]() ,求证:
,求证:![]() .
.
附: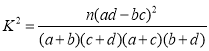
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |