Question

【题目】已知定义域为{x|x≠0}的偶函数f（x），其导函数为f′（x），对任意正实数x满足xf′（x）＞﹣2f（x），若g（x）=x2f（x），则不等式g（x）＜g（1﹣x）的解集是（ ）
A.（ ，+∞）
B.（﹣∞， ）
C.（﹣∞，0）∪（0， ）
D.（0， ）

Answer 1

【答案】C
【解析】解：∵f（x）是定义域为{x|x≠0}的偶函数，
∴f（﹣x）=f（x）．
对任意正实数x满足xf′（x）＞﹣2f（x），
∴xf′（x）+2f（x）＞0，
∵g（x）=x2f（x），
∴g′（x）=2xf（x）+x2f′（x）＞0．
∴函数g（x）在（0，+∞）上单调递增，
∴g（x）在（﹣∞，0）递减；
由不等式g（x）＜g（1﹣x），
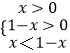∴ 或 ，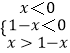
解得：0＜x＜ ，或x＜0
∴不等式g（x）＜g（1﹣x）的解集为：{x|0＜x＜ 或x＜0}．
故选：C．
【考点精析】利用导数的几何意义和利用导数研究函数的单调性对题目进行判断即可得到答案，需要熟知通过图像,我们可以看出当点趋近于时，直线与曲线相切．容易知道，割线的斜率是，当点趋近于时，函数在处的导数就是切线PT的斜率k，即；一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．