Question

【题目】已知函数，且．

（1）求的值；

（2）画出图像，并写出单调递增区间(不需要说明理由)；

（3）若，求的取值范围．

Answer 1

【答案】(1)；(2)图像见解析，（-∞，2）和（4，∞）（3）（8, 6+2）

【解析】

（1）利用f（4）=0，列出方程即可求实数m的值；

（2）化简函数的解析式，得到分段函数，然后作出函数f（x）的图象，根据图象直接指出f（x）的单调递减区间；

（3）借助函数图象的对称性，转化为求解c的取值范围．

（1）∵=x∣m-x∣,且)=0

∴ 4∣m-4∣=0

∴m=4

（2）f（x）=x|x﹣4|=，

f（x）的图象如图所示．

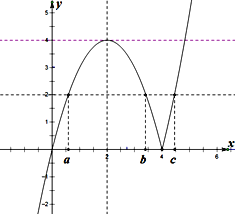
其单调增区间为：（-∞，2）和（4，∞）

（3）由图知： a+b=4为定值，即a+b+c的取值范围即为4+c的取值范围，

又∵当y=4时，x=2或x=2+2，

故c的取值范围为（4，2+2），

所以a+b+c的取值范围为（8, 6+2）