题目内容
已知数列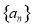 ,
,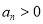 ,其前
,其前 项和
项和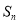 满足
满足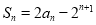 ,其中
,其中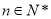 .
.
(1)设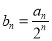 ,证明:数列
,证明:数列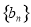 是等差数列;
是等差数列;
(2)设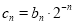 ,
,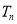 为数列
为数列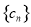 的前
的前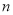 项和,求证:
项和,求证: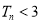 ;
;
(3)设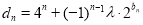 (
(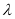 为非零整数,
为非零整数,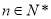 ),试确定
),试确定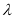 的值,使得对任意
的值,使得对任意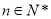 ,都有
,都有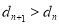 成立.
成立.
练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
题目内容
已知数列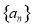 ,
,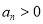 ,其前
,其前 项和
项和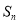 满足
满足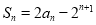 ,其中
,其中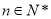 .
.
(1)设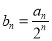 ,证明:数列
,证明:数列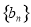 是等差数列;
是等差数列;
(2)设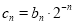 ,
,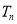 为数列
为数列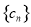 的前
的前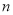 项和,求证:
项和,求证: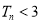 ;
;
(3)设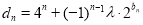 (
(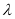 为非零整数,
为非零整数,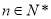 ),试确定
),试确定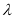 的值,使得对任意
的值,使得对任意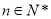 ,都有
,都有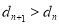 成立.
成立.
 口算题天天练系列答案
口算题天天练系列答案