题目内容
1.已知下面的数列通项和递推关系:①数列{an}(an=n)有递推关系an+2=2an+1-an;
②数列{bn}(bn=n2)有递推关系bn+3=3bn+2-3bn+1+bn;
③数列{cn}(cn=n3)有递推关系cn+4=4cn+3-6cn+2+4cn+1-cn;
④数列{dn}(dn=n4)有递推关系dn+5=5dn+4-10dn+3+10dn+2-5dn+1+dn;
试猜测:
数列{en}(en=n5)的类似的递推关系en+6=6en+5-15en+4+20en+3-15en+2+6en+1-en.
分析 由已知中数列{an}(an=n),数列{bn}(bn=n2),数列{cn}(cn=n3),数列{dn}(dn=n4)的递推关系,分析系数的变化规律,可得答案.
解答 解:由已知中:
①数列{an}(an=n)有递推关系an+2=2an+1-an;
②数列{bn}(bn=n2)有递推关系bn+3=3bn+2-3bn+1+bn;
③数列{cn}(cn=n3)有递推关系cn+4=4cn+3-6cn+2+4cn+1-cn;
④数列{dn}(dn=n4)有递推关系dn+5=5dn+4-10dn+3+10dn+2-5dn+1+dn;
…
归纳可得:数列{en}(en=n5)的类似的递推关系为:en+6=6en+5-15en+4+20en+3-15en+2+6en+1-en
故答案为:en+6=6en+5-15en+4+20en+3-15en+2+6en+1-en
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
9.已知 F1,F2分别是双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左,右焦点,过 F1,的直线l与双曲线的左右两支分别交于点A,B,若|AB|=|AF2|,∠F1AF2=90°,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{6}+\sqrt{3}}}{2}$ | B. | $\sqrt{6}+\sqrt{3}$ | C. | $\frac{{\sqrt{5+2\sqrt{2}}}}{2}$ | D. | $\sqrt{5+2\sqrt{2}}$ |
13.某校对数学、物理两科进行学业水平考前辅导,辅导后进行测试,按成绩(满分100分)划分为合格(成绩大于或等于70分)和不合格(成绩小于70分).现随机抽取两科各100名学生的成绩统计如下:
(1)试分别估计该校学生数学、物理合格的概率;
(2)数学合格一人可以赢得4小时机器人操作时间,不合格一人则减少1小时机器人操作
时间;物理合格一人可赢得5小时机器人操作时间,不合格一人则减少2小时机器人操作时间.在(1)的前提下,
(i)记X为数学一人和物理一人所赢得的机器人操作时间(单位:小时)总和,求随机变量X 的分布列和数学期望;
(ii)随机抽取5名学生,求这5名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于14小时的概率.
| 成绩(单位:分) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 数学 | 8 | 12 | 40 | 32 | 8 |
| 物理 | 7 | 18 | 40 | 29 | 6 |
(2)数学合格一人可以赢得4小时机器人操作时间,不合格一人则减少1小时机器人操作
时间;物理合格一人可赢得5小时机器人操作时间,不合格一人则减少2小时机器人操作时间.在(1)的前提下,
(i)记X为数学一人和物理一人所赢得的机器人操作时间(单位:小时)总和,求随机变量X 的分布列和数学期望;
(ii)随机抽取5名学生,求这5名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于14小时的概率.
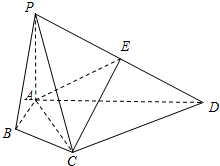 在四棱锥P-ABCD中,PA⊥平面ABCD,E是PD的中点,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,AC=AP.
在四棱锥P-ABCD中,PA⊥平面ABCD,E是PD的中点,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,AC=AP.
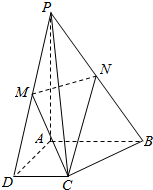 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.