题目内容
【题目】如图为我国数学家赵爽
约3世纪初
在为《周髀算经》作注时验证勾股定理的示意图，现在提供5种颜色给其中5个小区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不同，则
区域涂色不相同的概率为
A. 
B. 
C. 
D. 
【答案】B
【解析】
利用分步计数原理求出不同的涂色方案有420种，其中，
区域涂色不相同的情况有120种，由此根据古典概型概率公式能求出区域涂色不相同的概率．
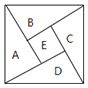
提供5种颜色给其中5个小区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不同，
根据题意，如图，设5个区域依次为
,分4步进行
，对于区域
，有5种颜色可选；
，对于区域
与区域相邻，有4种颜色可选；
，对于区域
，与
区域相邻，有3种颜色可选；
，对于区域
，若
与颜色相同，
区域有3种颜色可选，
若与颜色不相同，区域有2种颜色可选，区域有2种颜色可选，
则区域有
种选择，
则不同的涂色方案有
种，
其中，区域涂色不相同的情况有：
，对于区域，有5种颜色可选；
，对于区域与区域相邻，有4种颜色可选；
，对于区域与
区域相邻，有2种颜色可选；
，对于区域，若与颜色相同，区域有2种颜色可选，
若与颜色不相同，区域有1种颜色可选，区域有1种颜色可选，
则区域有
种选择，
不同的涂色方案有
种，
区域涂色不相同的概率为
,故选B．
阅读快车系列答案
【题目】2020年开始，国家逐步推行全新的高考制度．新高考不再分文理科，采用3+3模式，其中语文、数学、外语三科为必考科目，满分各150分，另外考生还要依据想考取的高校及专业的要求，结合自己的兴趣爱好等因素，在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试（6选3），每科目满分100分．为了应对新高考，某高中从高一年级1000名学生（其中男生550人，女生450人）中，根据性别分层，采用分层抽样的方法从中抽取100名学生进行调查．
（1）学校计划在高一上学期开设选修中的“物理”和“地理”两个科目，为了了解学生对这两个科目的选课情况，对抽取到的100名学生进行问卷调查（假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目），如表是根据调查结果得到的
列联表．请将列联表补充完整，并判断是否有
的把握认为选择科目与性别有关？说明你的理由；
（2）在抽取到的女生中按（1）中的选课情况进行分层抽样，从中抽出9名女生，再从这9名女生中随机抽取4人，设这4人中选择“地理”的人数为
，求的分布列及数学期望．
选择“物理” | 选择“地理” | 总计 | |
男生 | 10 | ||
女生 | 25 | ||
总计 |
附参考公式及数据：
，其中
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
【题目】“中国式过马路”存在很大的交通安全隐患，某调查机构为了解路人对“中国式过马路”的态度是否与性别有关，从马路旁随机抽取30名路人进行了问卷调查，得到了如图的
列联表．已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是
．
（1）求列联表中的
，
的值；
男性 | 女性 | 合计 | |
反感 | 10 |
|
|
不反感 |
| 8 |
|
合计 |
|
| 30 |
（2）根据列联表中的数据，判断是否有95%把握认为反感“中国式过马路”与性别有关？
临界值表：
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式：
，
