题目内容
已知函数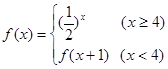 ,则
,则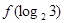 的值为 .
的值为 .
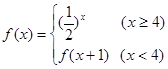 ,则
,则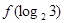 的值为 .
的值为 .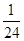
试题分析:根据题意可知,
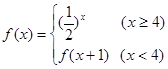 ,那么结合对数函数的性质可知
,那么结合对数函数的性质可知 ,因此那么可知
,因此那么可知
故答案为
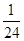
点评:根据已知的表达式求解函数值,要注意变量的取值范围,则要选择不同的解析式来计算,对于复合函数的求值,一般从内向外依次求解函数值得到结论,属于基础题。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
题目内容
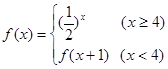 ,则
,则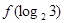 的值为 .
的值为 .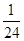
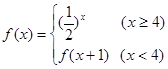 ,那么结合对数函数的性质可知
,那么结合对数函数的性质可知 ,因此那么可知
,因此那么可知
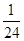

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案