题目内容
13.椭圆$\frac{x^2}{4}+\frac{y^2}{a^2}=1$与双曲线$\frac{{x}^{2}}{a}$-$\frac{{y}^{2}}{2}$=1有相同的焦点,则a的值为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
分析 确定a>0,且椭圆的焦点应该在x轴上,4-a2=a+2,即可求出a的值.
解答 解:因为椭圆$\frac{x^2}{4}+\frac{y^2}{a^2}=1$与双曲线$\frac{{x}^{2}}{a}$-$\frac{{y}^{2}}{2}$=1有相同的焦点,所以a>0,且椭圆的焦点应该在x轴上,
所以4-a2=a+2,所以a=-2,或a=1.
因为a>0,所以a=1.
故选:A.
点评 本小题主要考查椭圆与双曲线的标准方程及其应用.椭圆中c2=a2-b2,而在双曲线中,c2=a2+b2.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
8. 研究某设备的使用年限x与保养和维修费用y之间的关系,测得一组数据如下
研究某设备的使用年限x与保养和维修费用y之间的关系,测得一组数据如下
由数据可知y与x有明显的线性相关关系,附参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2-n{\overline{x}}^{2}}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
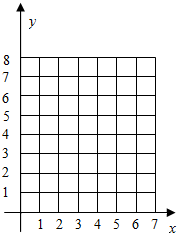
(1)将表中的数据画成散点图:
(2)试预测第7年的设备保养和维修费用.
 研究某设备的使用年限x与保养和维修费用y之间的关系,测得一组数据如下
研究某设备的使用年限x与保养和维修费用y之间的关系,测得一组数据如下| 年限x(年) | 2 | 3 | 4 | 5 | 6 |
| 保养和维修费用y(万元) | 3 | 3.5 | 5 | 6.5 | 7 |
(1)将表中的数据画成散点图:
(2)试预测第7年的设备保养和维修费用.
18.已知f(x)=x2+2xf′(1)-6,则f′(1)等于( )
| A. | 4 | B. | -2 | C. | 0 | D. | 2 |
5.已知复数z=$\frac{2+i}{i^3}$,z的共轭复数是$\overline{z}$,则$\overline{z}$对应的点位于复平面内的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.函数$y=\frac{{{{(x-1)}^0}}}{{\sqrt{|x|+x}}}$的定义域是( )
| A. | (0,+∞) | B. | (0,1)∪(1,+∞) | C. | (-∞,0) | D. | (-∞,-1)∪(0,+∞) |
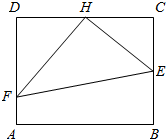 某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100米,宽BC=50$\sqrt{3}$米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE、HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.
某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100米,宽BC=50$\sqrt{3}$米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE、HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.