题目内容
已知函数f(x)是周期为4的偶函数,当x∈[0,2]时,f(x)=-x+1,则不等式x•f(x)>0在x∈(-3,1)上的解集为 .
考点:函数奇偶性的性质,函数的周期性
专题:计算题,数形结合,函数的性质及应用
分析:由函数的性质可得函数的图象,化不等式为x与f(x)同号,数形结合可得答案.
解答:
 解:依题意:函数f(x)是周期为4的偶函数,
解:依题意:函数f(x)是周期为4的偶函数,
当x∈[0,2]时,f(x)=-x+1,
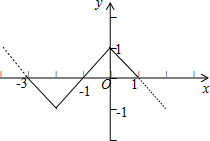
由此可作出函数f(x)在x∈(-3,1)的图象:
不等式x•f(x)>0在x∈(-3,1)上的解集
即图象上x与f(x)同号的区域,
由图可知当x∈(-3,-1)∪(0,1)时符合题意,
故答案为:(-3,-1)∪(0,1).
 解:依题意:函数f(x)是周期为4的偶函数,
解:依题意:函数f(x)是周期为4的偶函数,当x∈[0,2]时,f(x)=-x+1,
由此可作出函数f(x)在x∈(-3,1)的图象:
不等式x•f(x)>0在x∈(-3,1)上的解集
即图象上x与f(x)同号的区域,
由图可知当x∈(-3,-1)∪(0,1)时符合题意,
故答案为:(-3,-1)∪(0,1).
点评:本题考查函数的周期性和单调性,数形结合是解决问题的关键,属中档题.

练习册系列答案
相关题目
解下列不等式:
(1)|4x-3|<21;
(2)|
+2|≥
;
(3)
>
;
(4)|x+3|>x+3;
(5)|3x-4|>2x-1;
(6)|3x-4|≤x-1.
(1)|4x-3|<21;
(2)|
| x-1 |
| 2 |
| 3 |
| 4 |
(3)
| |3x-1|-1 |
| 2 |
| |1-3x|+1 |
| 3 |
(4)|x+3|>x+3;
(5)|3x-4|>2x-1;
(6)|3x-4|≤x-1.
设2b是1-a和1+a的等比中项,则a+4b的最大值为( )
| A、1 | ||||
| B、3 | ||||
C、
| ||||
D、
|
已知
,则
的最大值为( )
|
| y-2 |
| x-3 |
| A、2 | ||
B、
| ||
| C、0 | ||
D、
|
设f(x)在x0处可导,
的值是( )
| lim |
| △x→0 |
| f(x0-2△x)-f(x0) |
| △x |
| A、2f′(x0) |
| B、-f′(x0) |
| C、-2f′(x0) |
| D、不一定存在 |