题目内容
已知f(x)与g(x)都是定义在R上的奇函数,若F(x)=af(x)+bg(x)+2,且F(-2)=5,则F(2)= .
考点:函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:令h(x)=F(x)-2,证明函数h(x)为奇函数,再由F(-2)=5,求得h(-2)的值,可得h(2)的值,从而求得F(2)的值.
解答:
解:令h(x)=F(x)-2=af(x)+bg(x),
由于f(x)和g(x)都是定义在R上的奇函数,
故函数h(-x)=af(-x)+bg(-x)=-af(x)-bg(x)=-h(x),
故函数h(x)为奇函数.
再由F(-2)=5,可得h(-2)=F(-2)-2=5-2=3,
故h(-2)=-h(2)=3,则h(2)=-3,F(2)-2=-3,
求得F(2)=-1,
故答案为:-1.
由于f(x)和g(x)都是定义在R上的奇函数,
故函数h(-x)=af(-x)+bg(-x)=-af(x)-bg(x)=-h(x),
故函数h(x)为奇函数.
再由F(-2)=5,可得h(-2)=F(-2)-2=5-2=3,
故h(-2)=-h(2)=3,则h(2)=-3,F(2)-2=-3,
求得F(2)=-1,
故答案为:-1.
点评:本题主要考查利用函数的奇偶性求函数的值,属于中档题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
设变量x,y满足约束条件
,则目标函数z=2x+3y的最大值为( )
|
| A、22 | B、20 | C、5 | D、4 |
给出下列四个命题:
①若直线a∥平面α,直线b⊥α,则a⊥b;
②若直线a∥平面α,α⊥平面β,则a⊥β;
③若a、b是二条平行直线,b?平面α,则a∥α;
④若平面α⊥平面β,平面γ⊥β,则α∥γ.
其中不正确的命题的个数是( )
①若直线a∥平面α,直线b⊥α,则a⊥b;
②若直线a∥平面α,α⊥平面β,则a⊥β;
③若a、b是二条平行直线,b?平面α,则a∥α;
④若平面α⊥平面β,平面γ⊥β,则α∥γ.
其中不正确的命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
| ∫ |
-
|
| A、0 | ||
B、-
| ||
C、
| ||
| D、π |
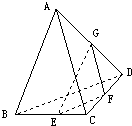 E、F、G分别是空间四边形ABCD的棱BC、CD、DA的中点,则此四面体中与过E、F、G的截面平行的棱的条数是( )
E、F、G分别是空间四边形ABCD的棱BC、CD、DA的中点,则此四面体中与过E、F、G的截面平行的棱的条数是( )