题目内容
【题目】如图所示,在四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
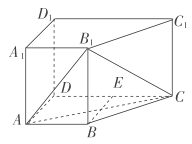
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,证明出四边形
,证明出四边形![]() 为平行四边形,由此可得出
为平行四边形,由此可得出![]() 各边边长,利用勾股定理逆定理可证明出
各边边长,利用勾股定理逆定理可证明出![]() ,进而得出
,进而得出![]() ,再由侧棱
,再由侧棱![]() 底面
底面![]() ,可得出
,可得出![]() ,利用线面垂直的判定定理可证明出
,利用线面垂直的判定定理可证明出![]() 平面
平面![]() ;
;
(2)以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 的方向为
的方向为![]() 、
、![]() 、
、![]() 轴的正方向建立空间直角坐标系,计算出平面
轴的正方向建立空间直角坐标系,计算出平面![]() 的一个法向量,利用空间向量法可求出直线
的一个法向量,利用空间向量法可求出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
![]() ,
,![]() ,
,![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() 且
且![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,即
,即![]() ,又
,又![]() ,所以
,所以![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
又![]() ,
,![]() 平面
平面![]() ;
;
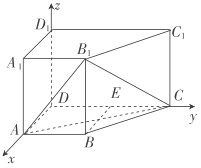
(2)以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 的方向为
的方向为![]() 、
、![]() 、
、![]() 轴的正方向建立如图所示的空间直角坐标系,则
轴的正方向建立如图所示的空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,则由
,则由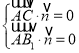 ,得
,得![]() ,
,
取![]() ,得
,得![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则 .
.
因此,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】“中国式过马路”的大意是凑够一撮人即可走,跟红绿灯无关.部分法律专家的观点为“交通规则的制定目的就在于服务城市管理,方便行人,而‘中国式过马路’是对我国法治化进程的严重阻碍,反应了国人规则意识的淡薄.”某新闻媒体对此观点进行了网上调查,所有参与调查的人中,持“支持”“中立”和“不支持”态度的人数如表所示:
支持 | 中立 | 不支持 | |
20岁以下 | 700 | 450 | 200 |
20岁及以上 | 200 | 150 | 300 |
在所有参与调查的人中,用分层随机抽样的方法抽取![]() 人,则持“支持”态度的人中20岁及以上的有_________人
人,则持“支持”态度的人中20岁及以上的有_________人