题目内容
【题目】设点P在曲线y=x2上,从原点向A(2,4)移动,如果直线OP,曲线y=x2及直线x=2所围成的面积分别记为S1、S2.
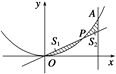
(1)当S1=S2时,求点P的坐标;
(2)当S1+S2有最小值时,求点P的坐标和最小值.
【答案】(1)![]() ,(2)
,(2)![]() ,
,![]()
【解析】
试题(1)可考虑用定积分求两曲线围成的封闭图形面积,直线OP的方程为y=tx,则S1为直线OP与曲线y=x2
当x∈(0,t)时所围面积,所以,S1=∫0t(tx﹣x2)dx,S2为直线OP与曲线y=x2当x∈(t,2)时所围面积,所以,
S2=∫t2(x2﹣tx)dx,再根据S1=S2就可求出t值.
(Ⅱ)由(2)可求当S1+S2,化简后,为t的三次函数,再利用导数求最小值,以及相应的x值,就可求出P点坐标为多少时,S1+S2有最小值.
试题解析:
(1)设点P的横坐标为t(0<t<2),则P点的坐标为(t,t2),
直线OP的方程为y=tx
S1=∫0t(tx﹣x2)dx=![]() ,S2=∫t2(x2﹣tx)dx=
,S2=∫t2(x2﹣tx)dx=![]() ,
,
因为S1=S2,,所以t=![]() ,点P的坐标为
,点P的坐标为![]()
(2)S=S1+S2=![]() =
=![]()
S′=t2﹣2,令S'=0得t2﹣2=0,t=![]()
因为0<t<![]() 时,S'<0;
时,S'<0;![]() <t<2时,S'>0
<t<2时,S'>0
所以,当t=![]() 时,Smin=
时,Smin=![]() ,P点的坐标为
,P点的坐标为![]() .
.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目