题目内容
【题目】如图,已知抛物线C:![]() ,过抛物线焦点F的直线交抛物线C于A,B两点,P是抛物线外一点,连接
,过抛物线焦点F的直线交抛物线C于A,B两点,P是抛物线外一点,连接![]() ,
,![]() 分别交抛物线于点C,D,且
分别交抛物线于点C,D,且![]() ,设
,设![]() ,
,![]() 的中点分别为M,N.
的中点分别为M,N.
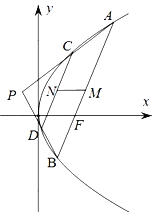
(1)求证:![]() 轴;
轴;
(2)若![]() ,求
,求![]() 面积的最小值.
面积的最小值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)设直线![]() 的方程为
的方程为![]() ,联立直线方程和抛物线方程,消去
,联立直线方程和抛物线方程,消去![]() 后利用韦达定理及中点坐标公式即可求得
后利用韦达定理及中点坐标公式即可求得![]() ,即可求得
,即可求得![]() 轴;
轴;
(2)根据向量的坐标运算及点在抛物线上,即可求得![]() ,根据三角形的面积公式即可求得
,根据三角形的面积公式即可求得![]() 面积的最小值.
面积的最小值.
(1)抛物线C:![]() 的焦点
的焦点![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
由![]() ,消去x,整理得
,消去x,整理得![]() ,
,
则![]() ,
,![]() ,
,![]() ,因为
,因为![]() ,
,
所以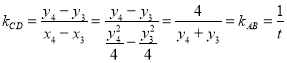 ,即
,即![]() ,
,
由![]() ,所以
,所以![]() 轴.
轴.
(2)由(1)可知,![]() ,
,![]() ,则
,则![]() ,
,
设![]() ,由
,由![]() ,
,![]() ,得
,得![]() ,
,![]() ,
,
代入抛物线![]() ,得到
,得到![]() ,
,
同理![]() ,
,
所以![]() ,
,![]() 为方程
为方程![]() ,
,
即![]() ,所以
,所以![]() ,
,
即M,N,P三点共线,
又![]() ,所以
,所以![]() ,
,
又![]() ,
,
所以![]() ,
,
当![]() ,
,![]() 面积的最小值
面积的最小值![]() .
.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
【题目】为了响应国家号召,某校组织部分学生参与了“垃圾分类,从我做起”的知识问卷作答,并将学生的作答结果分为“合格”与“不合格”两类与“问卷的结果”有关?
不合格 | 合格 | |
男生 | 14 | 16 |
女生 | 10 | 20 |
(1)是否有90%以上的把握认为“性别”与“问卷的结果”有关?
(2)在成绩合格的学生中,利用性别进行分层抽样,共选取9人进行座谈,再从这9人中随机抽取5人发送奖品,记拿到奖品的男生人数为X,求X的分布列及数学期望![]() .
.
附: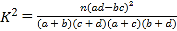
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.703 | 3.841 | 6.635 | 10.828 |