题目内容
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
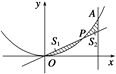
(2)已知圆方程为![]() ,过圆上任意一点作圆的切线,切线与椭圆
,过圆上任意一点作圆的切线,切线与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,设
为坐标原点,设![]() 为
为![]() 的中点,求
的中点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由题意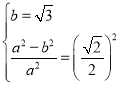 ,解方程组即可得解;
,解方程组即可得解;
(2)当切线斜率不存在时,易得![]() ;当切线斜率存在时,设切线方程为y=kx+m,点
;当切线斜率存在时,设切线方程为y=kx+m,点![]() ,点
,点![]() ,联立方程得
,联立方程得![]() ,
, ![]() ,由切线的性质得m2=2(1+k2),得到
,由切线的性质得m2=2(1+k2),得到![]() 关于k的表达式,当
关于k的表达式,当![]() 时,
时,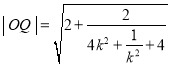 ,利用基本不等式即可得解.
,利用基本不等式即可得解.
(1)![]() 椭圆
椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() ,
,
![]()
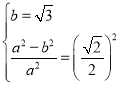 ,解得
,解得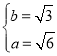 ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(2)由题得圆的圆心为![]() ,半径为
,半径为![]() ,
,
当切线斜率不存在时,切点即为![]() ,此时
,此时![]() ;
;
当切线斜率存在时,设切线方程为y=kx+m,A(x1,y1),B(x2,y2),
联立方程![]() ,得:(1+2k2)x2+4kmx+2m2﹣6=0,
,得:(1+2k2)x2+4kmx+2m2﹣6=0,
∴![]() ,
,![]() ,
,
∴![]() ∴Q(
∴Q(![]() ,
,![]() ),
),
∵直线AB 与圆O相切,∴![]() ,即m2=2(1+k2),
,即m2=2(1+k2),
∴ ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,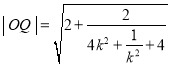 ,
,
![]()
![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,![]()
![]() .
.
综上,![]() 的取值范围为
的取值范围为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了响应国家号召,某校组织部分学生参与了“垃圾分类,从我做起”的知识问卷作答,并将学生的作答结果分为“合格”与“不合格”两类与“问卷的结果”有关?
不合格 | 合格 | |
男生 | 14 | 16 |
女生 | 10 | 20 |
(1)是否有90%以上的把握认为“性别”与“问卷的结果”有关?
(2)在成绩合格的学生中,利用性别进行分层抽样,共选取9人进行座谈,再从这9人中随机抽取5人发送奖品,记拿到奖品的男生人数为X,求X的分布列及数学期望![]() .
.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.703 | 3.841 | 6.635 | 10.828 |
【题目】体温是人体健康状况的直接反应,一般认为成年人腋下温度T(单位:![]() )平均在
)平均在![]() 之间即为正常体温,超过
之间即为正常体温,超过![]() 即为发热.发热状态下,不同体温可分成以下三种发热类型:低热:
即为发热.发热状态下,不同体温可分成以下三种发热类型:低热:![]() ;高热:
;高热:![]() ;超高热(有生命危险):
;超高热(有生命危险):![]() .某位患者因患肺炎发热,于12日至26日住院治疗.医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热.住院期间,患者每天上午8:00服药,护士每天下午16:00为患者测量腋下体温记录如下:
.某位患者因患肺炎发热,于12日至26日住院治疗.医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热.住院期间,患者每天上午8:00服药,护士每天下午16:00为患者测量腋下体温记录如下:
抗生素使用情况 | 没有使用 | 使用“抗生素A”疗 | 使用“抗生素B”治疗 | |||||
日期 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 |
体温( | 38.7 | 39.4 | 39.7 | 40.1 | 39.9 | 39.2 | 38.9 | 39.0 |
抗生素使用情况 | 使用“抗生素C”治疗 | 没有使用 | |||||
日期 | 20日 | 21日 | 22日 | 23日 | 24日 | 25日 | 26日 |
体温( | 38.4 | 38.0 | 37.6 | 37.1 | 36.8 | 36.6 | 36.3 |
(I)请你计算住院期间该患者体温不低于![]() 的各天体温平均值;
的各天体温平均值;
(II)在19日—23日期间,医生会随机选取3天在测量体温的同时为该患者进行某一特殊项目“a项目”的检查,记X为高热体温下做“a项目”检查的天数,试求X的分布列与数学期望;
(III)抗生素治疗一般在服药后2-8个小时就能出现血液浓度的高峰,开始杀灭细菌,达到消炎退热效果.假设三种抗生素治疗效果相互独立,请依据表中数据,判断哪种抗生素治疗效果最佳,并说明理由.