题目内容
已知函数 的图象在与
的图象在与 轴交点处的切线方程是
轴交点处的切线方程是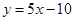 .
.
(I)求函数 的解析式;
的解析式;
(II)设函数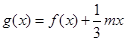 ,若
,若 的极值存在,求实数
的极值存在,求实数 的取值范围以及函数
的取值范围以及函数 取得极值时对应的自变量
取得极值时对应的自变量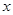 的值.
的值.
(I) ;(II)
;(II) 时,函数
时,函数 有极值;
有极值;
当 时,
时, 有极大值;当
有极大值;当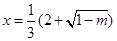 时,
时, 有极小值.
有极小值.
解析试题分析:(I)涉及切线,便要求出切点.本题中切点如何求?函数 的图象在与
的图象在与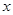 轴交点处的切线方程是
轴交点处的切线方程是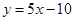 .说明切点就是直线
.说明切点就是直线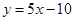 与
与 轴交点,所以令
轴交点,所以令 便得切点为(2,0).切点既在切线上又曲线,所以有
便得切点为(2,0).切点既在切线上又曲线,所以有 , 即
, 即 .
.
函数在切点处的导数就是切线的斜率,所以由已知有 即
即 .这样便得一个方程组,解这个方程组求出
.这样便得一个方程组,解这个方程组求出 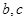 便
便 的解析式.
的解析式.
(II)将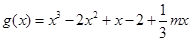 求导得,
求导得,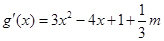 ,
,
令 .这是一个二次方程,要使得函数有极值,则方程要有两个不同的实数根,所以
.这是一个二次方程,要使得函数有极值,则方程要有两个不同的实数根,所以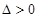 ,由此可得
,由此可得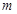 的范围.解方程
的范围.解方程 有便得取得极值时
有便得取得极值时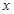 的值.
的值.
试题解析:( I)由已知,切点为(2,0), 故有 , 即
, 即
又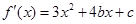 ,由已知
,由已知 得
得
联立①②,解得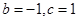 .所以函数的解析式为
.所以函数的解析式为
(II)因为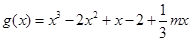
令
当函数有极值时,则 ,方程
,方程 有实数解, 由
有实数解, 由 ,得
,得 .
.
①当 时,
时,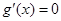 有实数
有实数 ,在
,在 左右两侧均有
左右两侧均有 ,故函数
,故函数 无极值
无极值
②当m<1时,g'(x)=0有两个实数根x1= (2-
(2- ), x2=
), x2= (2+
(2+ ), g(x),g'(x) 的情况如下表:
), g(x),g'(x) 的情况如下表: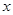

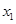
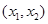
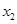

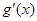
+ 0

优才精英口算题卡应用题系列答案
初中单元测试卷系列答案
朗朗阅读系列答案
同步练习册陕西科学技术出版社系列答案
应用题小状元应用题通关训练系列答案
考前小综合60练系列答案
考前专项分类高效检测系列答案

海东青跟踪测试系列答案
师说中考系列答案
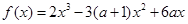
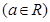 .
.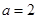 时,求函数
时,求函数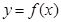 的单调区间;
的单调区间;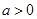 时,函数
时,函数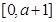 上的最大值为
上的最大值为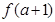 ,求
,求 的取值范围.
的取值范围.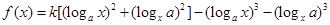 ,
,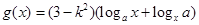 ,(其中
,(其中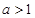 ),设
),设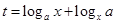 .
.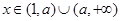 时,试将
时,试将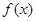 表示成
表示成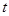 的函数
的函数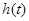 ,并探究函数
,并探究函数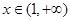 时,若存在
时,若存在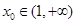 ,使
,使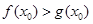 成立,试求
成立,试求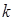 的范围.
的范围. (
( ,
,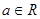 ),
), .
.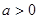 时,对于任意不相等的两个正实数
时,对于任意不相等的两个正实数 、
、 ,均有
,均有 成立;
成立;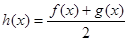 ,
,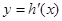 在
在 上单调递增,求实数
上单调递增,求实数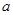 的取值范围;
的取值范围; .
. 的前
的前 项和为
项和为 ,已知
,已知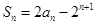 (n∈N*).
(n∈N*).
 ,数列
,数列 的前
的前 项和为
项和为 .利用(2)的结论证明:当n∈N*且n≥2时,
.利用(2)的结论证明:当n∈N*且n≥2时, .
.

 时,求
时,求 的单调区间;
的单调区间;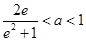 ,设
,设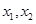 是函数
是函数 ,记
,记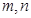 分别为
分别为 ,求实数
,求实数 的取值范围.
的取值范围.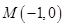 、
、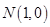 ,点
,点 为坐标平面内的动点,满足
为坐标平面内的动点,满足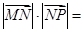
 .
.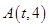 是动点
是动点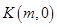 是
是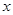 轴上的一动点,试讨论直线
轴上的一动点,试讨论直线 与圆
与圆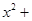
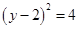 的位置关系.
的位置关系. ,
, .
. 时,函数
时,函数 取得极值,求
取得极值,求 的值;
的值; 时,求函数
时,求函数 时,关于
时,关于 的方程
的方程
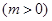 有唯一实数解,求实数
有唯一实数解,求实数 的值.
的值.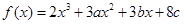 在
在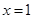 及
及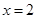 时取得极值.
时取得极值.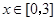 ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围.