题目内容
已知函数

(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若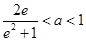 ,设
,设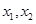 是函数
是函数 的两个极值点,且
的两个极值点,且 ,记
,记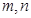 分别为
分别为 的极大值和极小值,令
的极大值和极小值,令 ,求实数
,求实数 的取值范围.
的取值范围.
(1)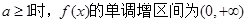 ;
;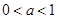 时,
时,
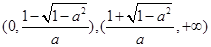 ,
,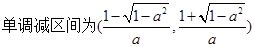 .(2)
.(2)
解析试题分析:(1)首先求出函数的导数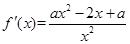 ,然后求出满足
,然后求出满足 或
或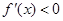 的区间即可.(2)根据极值点的概念得
的区间即可.(2)根据极值点的概念得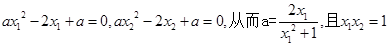 ,在由已知条件求出
,在由已知条件求出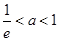 ,极值m,n的表达式,然后整理
,极值m,n的表达式,然后整理 =
= 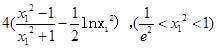 ,构造函数:令
,构造函数:令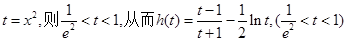 ,通过求导,证明
,通过求导,证明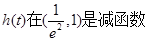 ,从而可得
,从而可得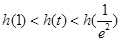 即可.
即可.
试题解析:(1) 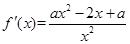 , 2分 令
, 2分 令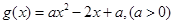 ,
, 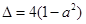
①.
②.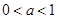 时,
时,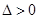 ,令
,令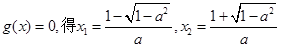
 ,
,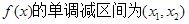 6分
6分
(2)依题意有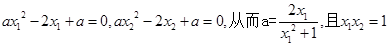
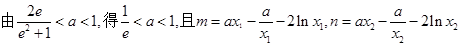
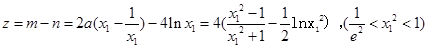 , 9分
, 9分
令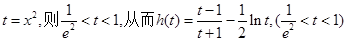 ,
,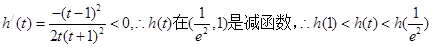
 13分
13分
考点:1.求函数的导数和导数的性质;2.导数的极值和导数性质的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
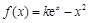 (其中
(其中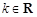 ,e是自然对数的底数).
,e是自然对数的底数).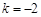 ,试判断函数
,试判断函数 在区间
在区间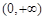 上的单调性;
上的单调性;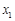 ,
,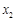 (
(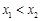 ),求k的取值范围;
),求k的取值范围;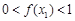 .
. 个月顾客对某种商品的需求总量
个月顾客对某种商品的需求总量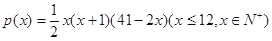 (单位:件)
(单位:件)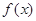 的表达式;
的表达式;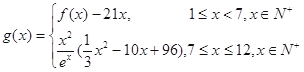 (单位:件),每件利润
(单位:件),每件利润 (单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据:
(单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据: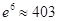 )
)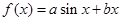 的图像在点
的图像在点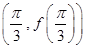 处的切线方程为
处的切线方程为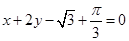 .
. ,
,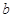 的值;
的值;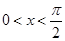 时,
时,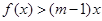 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的图象在与
的图象在与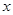 轴交点处的切线方程是
轴交点处的切线方程是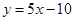 .
. 的解析式;
的解析式;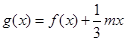 ,若
,若 的极值存在,求实数
的极值存在,求实数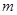 的取值范围以及函数
的取值范围以及函数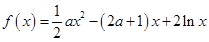 .
. 在
在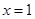 和
和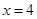 处的切线相互平行,求
处的切线相互平行,求 的值;
的值;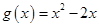 ,对任意的
,对任意的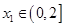 ,均存在
,均存在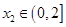 ,使得
,使得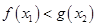 .试求实数
.试求实数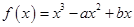 的图象与直线
的图象与直线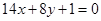 相切于点
相切于点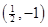 .
. 和
和 的值; (2)求
的值; (2)求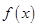 的极值.
的极值.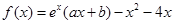 ,曲线
,曲线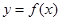 在点
在点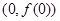 处切线方程为
处切线方程为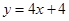 .
.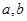 的值;
的值;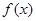 的单调性,并求
的单调性,并求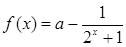 .
.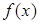 存在零点,求
存在零点,求 的取值范围
的取值范围 ,使
,使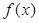 为奇函数?如果存在,求
为奇函数?如果存在,求