题目内容
学校餐厅每天供应500名学生用餐,每星期一有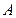 、
、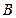 两种菜可供选择.调查资料表明,凡是在这星期一选
两种菜可供选择.调查资料表明,凡是在这星期一选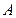 种菜的,下星期一会有
种菜的,下星期一会有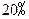 改选
改选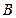 种菜;而选
种菜;而选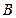 种菜的,下星期一有
种菜的,下星期一有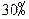 改选
改选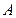 种菜.用
种菜.用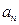 ,
,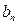 分别表示在第
分别表示在第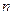 个星期选
个星期选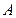 的人数和选
的人数和选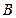 的人数,如果
的人数,如果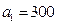 ,求
,求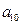
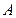 、
、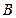 两种菜可供选择.调查资料表明,凡是在这星期一选
两种菜可供选择.调查资料表明,凡是在这星期一选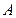 种菜的,下星期一会有
种菜的,下星期一会有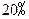 改选
改选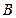 种菜;而选
种菜;而选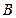 种菜的,下星期一有
种菜的,下星期一有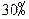 改选
改选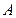 种菜.用
种菜.用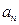 ,
,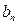 分别表示在第
分别表示在第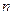 个星期选
个星期选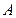 的人数和选
的人数和选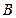 的人数,如果
的人数,如果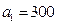 ,求
,求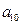
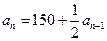 ,
,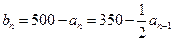 ;
;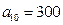
第一星期选择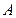 种菜的人数为
种菜的人数为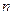 ,即
,即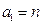 ,选择
,选择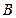 种菜的人数为
种菜的人数为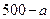 .
.
所以有以下关系式: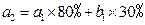 ,
,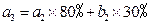 ,...,
,...,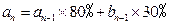 ,
,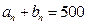 ,所以,
,所以,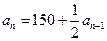 ,
,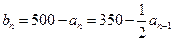 .
.
如果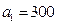 ,则
,则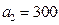 ,
, ,
, ,
,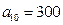 .
.
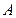 种菜的人数为
种菜的人数为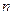 ,即
,即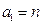 ,选择
,选择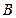 种菜的人数为
种菜的人数为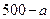 .
.所以有以下关系式:
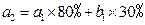 ,
,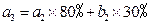 ,...,
,...,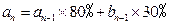 ,
,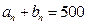 ,所以,
,所以,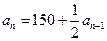 ,
,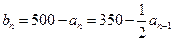 .
.如果
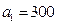 ,则
,则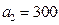 ,
, ,
, ,
,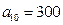 .
.
练习册系列答案
相关题目
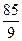 ,求这5个数.
,求这5个数. 中,设
中,设 .
. 为公差的等差数列,求证
为公差的等差数列,求证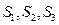 也是等差数列,并求其公差;
也是等差数列,并求其公差;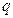 为公比的等比数列,求证
为公比的等比数列,求证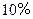 ,那么从今年起大约几年可使总销售量达到30000台(结果保留到个位)?
,那么从今年起大约几年可使总销售量达到30000台(结果保留到个位)? 的各项均为正数,其前
的各项均为正数,其前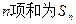 ,且
,且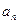 与1的等差中项等于
与1的等差中项等于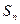 与
与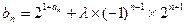 ,且数列
,且数列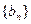 是单调递增数列。试求实数
是单调递增数列。试求实数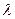 的取值范围。
的取值范围。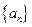 是等差数列.
是等差数列.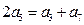 是否成立?
是否成立?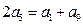 呢?为什么?
呢?为什么?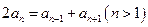 是否成立?据此你能得出什么结论?
是否成立?据此你能得出什么结论?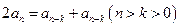 是否成立?你又能得出什么结论?
是否成立?你又能得出什么结论?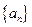 的首项
的首项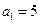 ,前
,前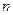 项和为
项和为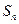 ,且
,且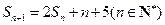 .
.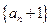 是等比数列;
是等比数列;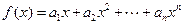 ,求函数
,求函数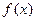 在点
在点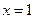 处的导数
处的导数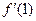 ,并比较
,并比较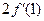 与
与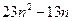 的大小.
的大小.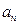 表示第
表示第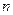 排的座位数吗?第10排能坐多少个人?
排的座位数吗?第10排能坐多少个人?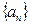 的前n项和为
的前n项和为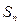 ,对于任意正整数n,都有等式:
,对于任意正整数n,都有等式: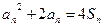 成立,求
成立,求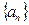 的通项an.
的通项an.