��Ŀ����
����Ŀ��ij���չ�˾�����ҵְ���Ƴ�һ�������ղ�Ʒ��ÿ��ÿ��ֻҪ���������ѣ�����������һ���Ի���50��Ԫ�����չ�˾��ְ�����µ����и�λ����ΪA��B��C����֣�������ʷ����ͳ�Ƴ�����ֵ�ÿ�⸶Ƶ�����±������Դ˹����⸶���ʣ���
������� | A | B | C |
�⸶Ƶ�� | | | |
�����ݹ涨���ò�Ʒ�����ֱ��������������ó������ѵ�20%���Էֱ�ȷ�������ÿ�ű������ѵ����ޣ�
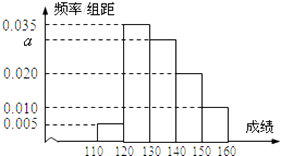
����ij��ҵ����ְ��20000�ˣ���������ֵ������ֲ�������ͼ���ϰ���Ϊȫ��ְ��ÿ�˹���һ�ݴ��ֱ��գ����ԣ����м���ĸ��ౣ���������Թ��Ʊ��չ�˾�����ڽ����е���������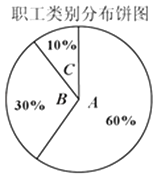
���𰸡��⣺�����蹤��A��ÿ�ݱ�������ΪaԪ���豣�չ�˾ÿ��������Ϊ�������X��
��X�ķֲ���Ϊ��
X | a | a��50��104 |
P | 1�� | |
���չ�˾��������Ϊ ![]() =a��5
=a��5
���ݹ���a��5��0.2a
���a��6.25Ԫ��
�蹤��B��ÿ�ݱ�������ΪbԪ���⸶������ֵΪ ![]() Ԫ��
Ԫ��
���չ�˾��������Ϊb��10Ԫ�����ݹ���b��10��0.2b�����b��12.5Ԫ��
�蹤��C��ÿ�ݱ�������ΪcԪ���⸶������ֵΪ ![]() Ԫ��
Ԫ��
���չ�˾��������Ϊc��50Ԫ�����ݹ���c��50��0.2c�����c��62.5Ԫ��
������A���Ʒ�ķ���Ϊ20000��60%=12000�ݣ�
����B���Ʒ�ķ���Ϊ20000��30%=6000�ݣ�
����C���Ʒ�ķ���Ϊ20000��10%=2000�ݣ�
��ҵ֧�����ܱ���Ϊ12000��6.25+6000��12.5+2000��62.5=275000Ԫ��
���չ�˾�����ڽ����е���������Ϊ275000��20%=55000Ԫ��
�������������蹤��A��ÿ�ݱ�������ΪaԪ���豣�չ�˾ÿ��������Ϊ�������X�����X�ķֲ��кͱ��չ�˾�������棬���ݹ���a��5��0.2a���Ӷ�a��6.25Ԫ���蹤��B��ÿ�ݱ�������ΪbԪ������⸶������ֵΪ10Ԫ�����չ�˾��������Ϊb��10Ԫ�����ݹ���b��10��0.2b�����b��12.5Ԫ���蹤��C��ÿ�ݱ�������ΪcԪ������⸶������ֵΪ50Ԫ�����չ�˾��������Ϊc��50Ԫ�����ݹ���c��50��0.2c�����c��62.5Ԫ��������A���Ʒ�ķ���Ϊ12000�ݣ�����B���Ʒ�ķ���Ϊ6000�ݣ�����C���Ʒ�ķ���Ϊ2000�ݣ��ɴ���������չ�˾�����ڽ����е���������
�����㾫����������Ĺؼ�����������ɢ�������������ֲ��е����֪ʶ���������������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��У�