题目内容
【题目】已知数列{an}满足a1=1,an+1=an+2,数列{bn}的前n项和为Sn , 且Sn=2﹣bn .
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=anbn , 求数列{cn}的前n项和Tn .
【答案】解:(Ⅰ)因为a1=1,an+1﹣an=2,
所以{an}为首项是1,公差为2的等差数列,
所以an=1+(n﹣1)×2=2n﹣1,
又当n=1时,b1=S1=2﹣b1,所以b1=1,
当n≥2时,Sn=2﹣bn①,Sn﹣1=2﹣bn﹣1②
由①﹣②得bn=﹣bn+bn﹣1,即 ![]() ,
,
所以{bn}是首项为1,公比为 ![]() 的等比数列,
的等比数列,
故 ![]() ,n∈N*;
,n∈N*;
(Ⅱ)由(Ⅰ)知 ![]() ,
,
则 ![]() ①,
①,
![]() =
= ![]() ②,
②,
①﹣②得 ![]()
= ![]() =
= 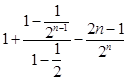 =
= ![]() .
.
所以 ![]() .
.
【解析】(Ⅰ)由等差数列的定义和通项公式可得an;运用数列的递推式:当n=1时,b1=S1,当n≥2时,bn=Sn﹣Sn﹣1,即可得到{bn}的通项公式;(Ⅱ)由(Ⅰ)知 ![]() ,运用数列的求和方法:错位相减法,结合等比数列的求和公式,即可得到所求和.
,运用数列的求和方法:错位相减法,结合等比数列的求和公式,即可得到所求和.
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系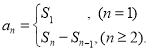 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

 阅读快车系列答案
阅读快车系列答案【题目】已知函数f(x)=|x﹣a|,其中a>1
(1)当a=2时,求不等式f(x)≥4﹣|x﹣4|的解集;
(2)已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.
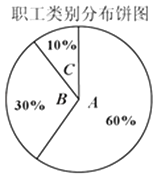
【题目】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
工种类别 | A | B | C |
赔付频率 | | | |
(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.