题目内容
11.已知定义在R上的函数y=f(x)对任意x都有f(x+1)=-f(x),当x∈[-1,1]时,f(x)=x2,函数g(x)=f(x)-loga|x|(a>0,a≠1)恰有8个零点,则a的值为5.分析 由题意,作出函数y=f(x)的图象,转化函数g(x)=f(x)-loga|x|的零点为图象的交点,从而求解.
解答 解:∵定义在R上的函数y=f(x)对任意x都有f(x+1)=-f(x),
∴f(x+2)=f[(x+1)=1]=-f(x+1)=f(x),
即函数f(x)是周期为2的周期函数,
若函数g(x)=f(x)-loga|x|(a>0,a≠1)恰有8个零点,
则函数y=f(x)与y=loga|x|(a>0,a≠1)的图象恰有8个交点,
又由x∈[-1,1]时,f(x)=x2,
故在同一坐标系可作出函数y=f(x)与y=loga|x|(a>0,a≠1)的图象如下: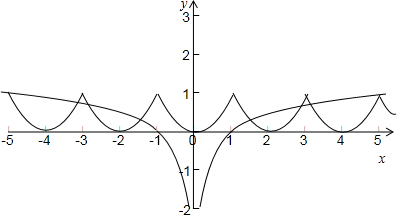
由图可知:函数y=f(x)与y=loga|x|(a>0,a≠1)的图象有8个交点时,
loga5=1,解得:a=5.
故答案为:5
点评 本题考查了学生的作图能力及识图能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.命题p:?x∈R,x2+1≥0的否定是( )
| A. | ¬p:?x∈R,x2+1<0 | B. | ¬p:?x∈R,x2+1<0 | C. | ¬p:?x∈R,x2+1≥0 | D. | ¬p:?x∈R,x2+1≤0 |
16.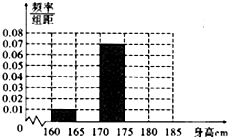 为了解我市大学生的体质状况,对昆明地区部分大学的学生进行了身高、体重和肺活量的抽样调查.现随机抽取100名学生,测得其身高情况如表所示.
为了解我市大学生的体质状况,对昆明地区部分大学的学生进行了身高、体重和肺活量的抽样调查.现随机抽取100名学生,测得其身高情况如表所示.
(Ⅰ)求出频率分布表中①、②、③位置上相应的数据,并补全图3所示频率分布直方图,再根据频率分布直方图估计众数的值;
(Ⅱ)若按身高分层抽样,抽取20人参加2015年庆元旦全民健身运动,其中有3名学生参加越野比赛,记这3名学生中“身高低于170cm”的人数为ξ,求ξ的分布列及数学期望.
 为了解我市大学生的体质状况,对昆明地区部分大学的学生进行了身高、体重和肺活量的抽样调查.现随机抽取100名学生,测得其身高情况如表所示.
为了解我市大学生的体质状况,对昆明地区部分大学的学生进行了身高、体重和肺活量的抽样调查.现随机抽取100名学生,测得其身高情况如表所示.| 分组 | 频数 | 频率 |
| [160,165) | ① | 0.050 |
| [165,170) | 20 | 0.200 |
| [170,175) | ② | ③ |
| [175,180) | 30 | 0.300 |
| [180,185] | 10 | 0.100 |
| 合 计 | 100 | 1.000 |
(Ⅱ)若按身高分层抽样,抽取20人参加2015年庆元旦全民健身运动,其中有3名学生参加越野比赛,记这3名学生中“身高低于170cm”的人数为ξ,求ξ的分布列及数学期望.
3.为了庆祝六一儿童节,某食品厂制作了3种不同的精美卡片,每袋食品随机装入一张卡片,集齐3种卡片可获奖,现购买5袋该产品,则获奖的概率为( )
| A. | $\frac{31}{81}$ | B. | $\frac{11}{27}$ | C. | $\frac{16}{27}$ | D. | $\frac{50}{81}$ |
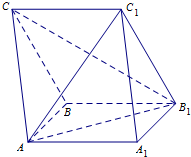 如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C是菱形,平面AA1B1B⊥平面BB1C1C.
如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C是菱形,平面AA1B1B⊥平面BB1C1C.