题目内容
短轴长为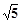 ,离心率e=
,离心率e=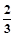 的椭圆的两焦点为F1、F2,过F1作直线交椭圆于A、B两点,则△ABF2周长为_____________。
的椭圆的两焦点为F1、F2,过F1作直线交椭圆于A、B两点,则△ABF2周长为_____________。
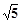 ,离心率e=
,离心率e=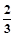 的椭圆的两焦点为F1、F2,过F1作直线交椭圆于A、B两点,则△ABF2周长为_____________。
的椭圆的两焦点为F1、F2,过F1作直线交椭圆于A、B两点,则△ABF2周长为_____________。12
试题分析:根据题意,由于短轴长为
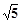 ,离心率e=
,离心率e=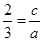 ,则可知b=
,则可知b=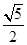 ,那么结合
,那么结合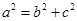 解得a=3,那么根据椭圆 定义可知,∵过点F1作直线l交椭圆于A、B两点,∴△ABF2的周长为4a=12,故答案为12.
解得a=3,那么根据椭圆 定义可知,∵过点F1作直线l交椭圆于A、B两点,∴△ABF2的周长为4a=12,故答案为12.点评:本题考查椭圆的几何性质,考查椭圆定义的运用,属于基础题

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 的两个端点
的两个端点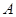 、
、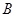 分别分别在
分别分别在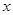 轴、
轴、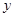 轴上滑动,
轴上滑动,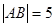 ,点
,点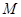 是
是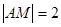 ,点
,点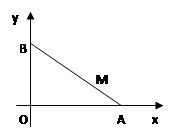
 为点
为点 为右焦点,过
为右焦点,过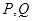 两点,求
两点,求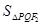 的最大值,并求此时直线
的最大值,并求此时直线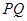 的方程.
的方程.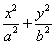 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为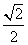 ,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(
,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(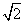 +1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
+1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D. 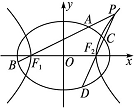
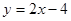 与抛物线
与抛物线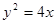 交于
交于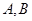 两点.
两点.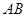 的长;(2)若抛物线
的长;(2)若抛物线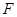 ,求
,求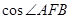 的值.
的值.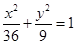 的弦被点
的弦被点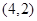 平分,则此弦所在的直线方程是 ( )
平分,则此弦所在的直线方程是 ( )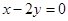
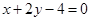
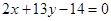
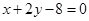
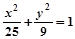 (y≠0)
(y≠0)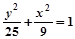 (y≠0)
(y≠0)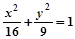 (y≠0)
(y≠0)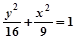 (y≠0)
(y≠0)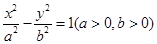 与椭圆
与椭圆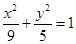 有相同的焦点
有相同的焦点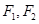 ,且该双曲线
,且该双曲线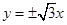 .
.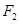 作斜率不为零的直线与此双曲线的左,右两支分别交于点
作斜率不为零的直线与此双曲线的左,右两支分别交于点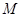 、
、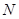 ,
,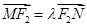 ,当
,当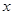 轴上的点
轴上的点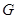 满足
满足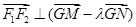 时,求点
时,求点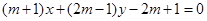 经过的定点的坐标是 .
经过的定点的坐标是 .