题目内容
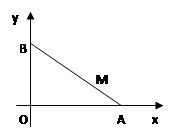
如图,线段 的两个端点
的两个端点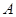 、
、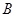 分别分别在
分别分别在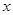 轴、
轴、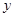 轴上滑动,
轴上滑动,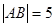 ,点
,点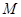 是
是 上一点,且
上一点,且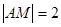 ,点
,点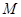 随线段
随线段 的运动而变化.
的运动而变化.
(1)求点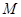 的轨迹方程;
的轨迹方程;
(2)设 为点
为点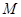 的轨迹的左焦点,
的轨迹的左焦点, 为右焦点,过
为右焦点,过 的直线交
的直线交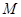 的轨迹于
的轨迹于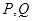 两点,求
两点,求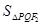 的最大值,并求此时直线
的最大值,并求此时直线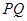 的方程.
的方程.
 的两个端点
的两个端点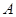 、
、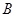 分别分别在
分别分别在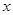 轴、
轴、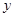 轴上滑动,
轴上滑动,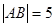 ,点
,点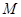 是
是 上一点,且
上一点,且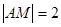 ,点
,点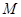 随线段
随线段 的运动而变化.
的运动而变化.
(1)求点
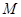 的轨迹方程;
的轨迹方程;(2)设
 为点
为点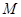 的轨迹的左焦点,
的轨迹的左焦点, 为右焦点,过
为右焦点,过 的直线交
的直线交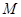 的轨迹于
的轨迹于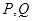 两点,求
两点,求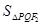 的最大值,并求此时直线
的最大值,并求此时直线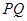 的方程.
的方程.(1) 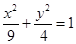 (2) PQ的方程为
(2) PQ的方程为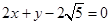 或
或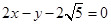
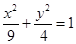 (2) PQ的方程为
(2) PQ的方程为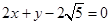 或
或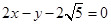
试题分析:解:(1)由题可知点
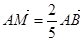 ,且可设A(
,且可设A(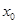 ,0),M(
,0),M(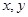 ),B(0,
),B(0,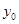 ),
),则可得
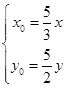 ,
, 又
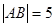 ,即
,即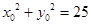 ,∴
,∴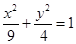 ,这就是点M的轨迹方程。
,这就是点M的轨迹方程。 (2)由(1)知
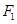 为(
为(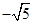 ,0),
,0),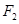 为(
为(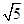 ,0),
,0),由题设PQ为
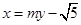 ,由
,由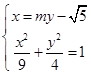 有
有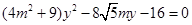 ,设
,设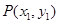 ,
, ,
,则
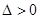 恒成立,
恒成立,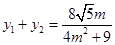 且
且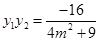 ,
,∴
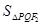 =
=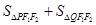 =
=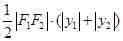
=
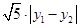 =
=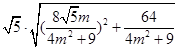 =
=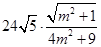
令
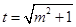 (
(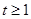 ),则
),则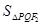 =
=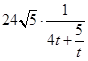
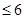 ,当且仅当
,当且仅当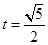 ,即
,即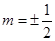 时取“=”∴
时取“=”∴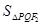 的最大值为6,此时PQ的方程为
的最大值为6,此时PQ的方程为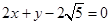 或
或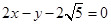
点评:解决的关键是利用向量的关系式来求解坐标关系,得到轨迹方程,同时能结合韦达定理来得到根与系数的关系来求解,属于基础题。

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 ,
,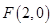 ,动点
,动点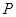 满足
满足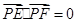 ,由点
,由点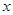 轴作垂线段
轴作垂线段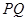 ,垂足为
,垂足为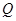 ,点
,点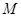 满足
满足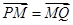 ,点
,点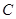 .
.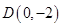 作直线
作直线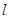 与曲线
与曲线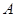 ,
,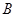 两点,点
两点,点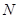 满足
满足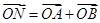 (
(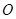 为原点),求四边形
为原点),求四边形 面积的最大值,并求此时的直线
面积的最大值,并求此时的直线
 .
. ),判断点P与直线L的位置关系;
),判断点P与直线L的位置关系;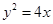 的焦点为圆心,且过坐标原点的圆的方程为( )
的焦点为圆心,且过坐标原点的圆的方程为( )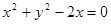
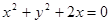
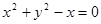
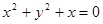
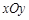 中,一直角三角形
中,一直角三角形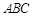 ,
,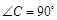 ,B、D在
,B、D在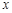 轴上且关于原点
轴上且关于原点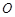 对称,
对称,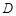 在边
在边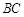 上,BD=3DC,△ABC的周长为12.若一双曲线
上,BD=3DC,△ABC的周长为12.若一双曲线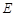 以B、C为焦点,且经过A、D两点.
以B、C为焦点,且经过A、D两点.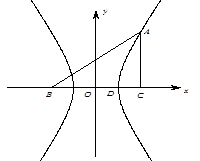
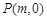 (
(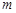 为非零常数)的直线
为非零常数)的直线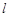 与双曲线
与双曲线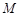 、
、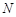 ,且
,且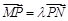 ,问在
,问在 ,使
,使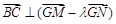 ?若存在,求出所有这样定点
?若存在,求出所有这样定点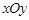 中,双曲线中心在原点,焦点在
中,双曲线中心在原点,焦点在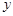 轴上,一条渐近线方程为
轴上,一条渐近线方程为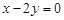 ,
,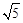
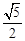
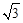
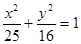 上的一点P,到椭圆一个焦点的距离为3,则P到另一焦点距离为( )
上的一点P,到椭圆一个焦点的距离为3,则P到另一焦点距离为( )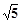 ,离心率e=
,离心率e=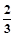 的椭圆的两焦点为F1、F2,过F1作直线交椭圆于A、B两点,则△ABF2周长为_____________。
的椭圆的两焦点为F1、F2,过F1作直线交椭圆于A、B两点,则△ABF2周长为_____________。