题目内容
设同时满足条件:①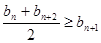 ;②
;②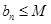 (
(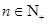 ,
,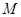 是与
是与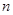 无关的常数)的无穷数列
无关的常数)的无穷数列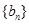 叫“嘉文”数列.已知数列
叫“嘉文”数列.已知数列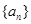 的前
的前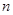 项和
项和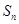 满足:
满足: 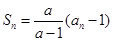 (
(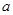 为常数,且
为常数,且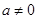 ,
,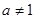 ).
).
(Ⅰ)求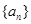 的通项公式;
的通项公式;
(Ⅱ)设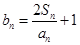 ,若数列
,若数列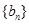 为等比数列,求
为等比数列,求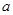 的值,并证明此时
的值,并证明此时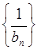 为“嘉文”数列.
为“嘉文”数列.
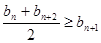 ;②
;②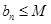 (
(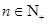 ,
,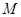 是与
是与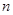 无关的常数)的无穷数列
无关的常数)的无穷数列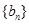 叫“嘉文”数列.已知数列
叫“嘉文”数列.已知数列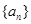 的前
的前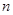 项和
项和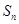 满足:
满足: 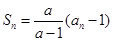 (
(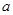 为常数,且
为常数,且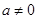 ,
,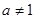 ).
). (Ⅰ)求
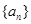 的通项公式;
的通项公式;(Ⅱ)设
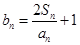 ,若数列
,若数列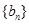 为等比数列,求
为等比数列,求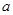 的值,并证明此时
的值,并证明此时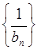 为“嘉文”数列.
为“嘉文”数列.(I)∴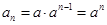 .
.
(II)由(I)知,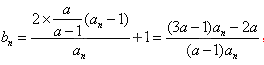 ,
,
若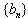 为等比数列,则有
为等比数列,则有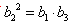 ,而
,而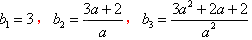 。
。
故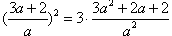 ,解得
,解得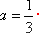 ,再将
,再将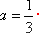 代入得:
代入得: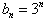 ,其为等比数列,所以
,其为等比数列,所以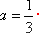 成立。由于①
成立。由于①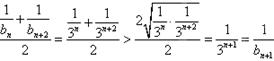 。
。
②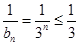 ,故存在
,故存在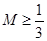 ;
;
所以符合①②,故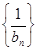 为“嘉文”数列。
为“嘉文”数列。
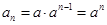 .
.(II)由(I)知,
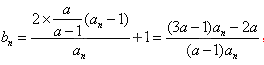 ,
,若
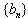 为等比数列,则有
为等比数列,则有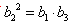 ,而
,而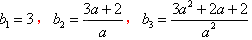 。
。故
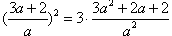 ,解得
,解得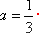 ,再将
,再将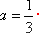 代入得:
代入得: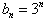 ,其为等比数列,所以
,其为等比数列,所以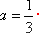 成立。由于①
成立。由于①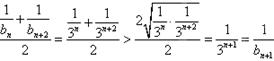 。
。②
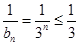 ,故存在
,故存在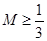 ;
;所以符合①②,故
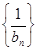 为“嘉文”数列。
为“嘉文”数列。本试题主要是考查了数列的通项公式的求解和数列的求和的运用以及等比数列定义问题。
(1)根据前n项和与通项公式的 关系得到数列的通项公式。
(2)根据新定义和第一问的结论来判定数列是否符合题意
(1)根据前n项和与通项公式的 关系得到数列的通项公式。
(2)根据新定义和第一问的结论来判定数列是否符合题意

练习册系列答案
相关题目
 满足
满足 和
和 ,则
,则
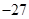
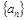 的前n项和为Sn,若S10=2,S30=14,则S20等于
的前n项和为Sn,若S10=2,S30=14,则S20等于 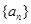 是首项为19,公差d=-2的等差数列,
是首项为19,公差d=-2的等差数列,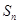 为
为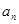 及
及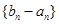 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列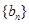 的通项公式及其前n项和
的通项公式及其前n项和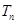
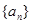 中,
中,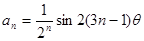 ,其中
,其中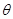 为方程
为方程 的解,则这个数列的前
的解,则这个数列的前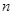 项和
项和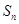 为( )
为( )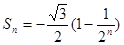

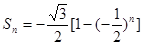
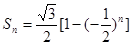
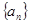 中,
中,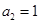 ,则其前3项的和
,则其前3项的和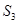 的取值范围是
的取值范围是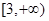
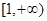
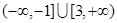
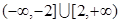
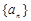 中,若公比
中,若公比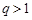 ,且
,且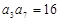 ,
,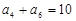 ,则
,则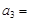
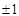
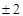
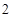
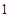
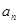 }中,
}中,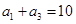 ,
,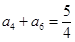 ,则等比数列{
,则等比数列{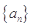 中,
中,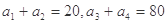 ,则
,则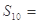 __________
__________