题目内容
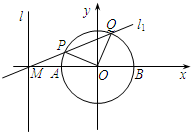 已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点(如图).
已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点(如图).(1)过M点的直线l1交圆于P、Q两点,且圆孤PQ恰为圆周的
| 1 |
| 4 |
(2)求以l为准线,中心在原点,且与圆O恰有两个公共点的椭圆方程.
考点:直线与圆锥曲线的综合问题
专题:计算题,圆锥曲线中的最值与范围问题
分析:(1)由圆孤PQ为圆周的
可求得O点到直线l1的距离为
,从而设l1的方程为y=k(x+2),由点到直线的距离公式求直线方程即可;
(2)设椭圆方程为
+
=1(a>b>0),从而可得
=2,由椭圆与圆O恰有两个不同的公共点可得b=1,从而求椭圆方程.
| 1 |
| 4 |
| ||
| 2 |
(2)设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
解答:
解:(1)∵圆孤PQ为圆周的
,
∴∠POQ=
,
∴O点到直线l1的距离为
.
设l1的方程为y=k(x+2),
∴
=
,
∴k2=
,
∴l1的方程为y=±
(x+2);
(2)设椭圆方程为
+
=1(a>b>0),
半焦距为c,则
=2,
∵椭圆与圆O恰有两个不同的公共点,则b=1.
∴b2+c2=2c,∴c=1,
∴a2=b2+c2=2.
∴所求椭圆方程为
+y2=1.
| 1 |
| 4 |
∴∠POQ=
| π |
| 2 |
∴O点到直线l1的距离为
| ||
| 2 |
设l1的方程为y=k(x+2),
∴
| |2k| | ||
|
| ||
| 2 |
∴k2=
| 1 |
| 7 |
∴l1的方程为y=±
| ||
| 7 |
(2)设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
半焦距为c,则
| a2 |
| c |
∵椭圆与圆O恰有两个不同的公共点,则b=1.
∴b2+c2=2c,∴c=1,
∴a2=b2+c2=2.
∴所求椭圆方程为
| x2 |
| 2 |
点评:本题考查了圆锥曲线与直线的位置关系及数形结合的数学思想应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
m取何实数时,复数Z=
+(m2-2m-15)i是纯虚数?( )
| m2-m-6 |
| m+3 |
| A、m=3或m=-2 |
| B、m=3 |
| C、m=-2 |
| D、m=-3或m=2 |
若a∈R,则方程x2+4y2sina=1所表示的曲线一定不是( )
| A、直线 | B、圆 | C、抛物线 | D、双曲线 |
椭圆
+
=1上的点M到左焦点F1的距离是2,N是MF1的中点,O为坐标原点,则|ON|为( )
| x2 |
| 25 |
| y2 |
| 9 |
| A、4 | ||
| B、2 | ||
| C、8 | ||
D、
|
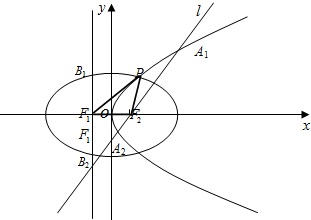 如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1、F2为焦点,离心率e=
如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1、F2为焦点,离心率e=