题目内容
已知等差数列{xn},Sn是{xn}的前n和,且x3=5,S5+x5=34
(1)求{xn}的通项公式;
(2)判别方程sin2xn+xncosxn+1=Sn是否有解,说明理由.
(3)设an=(
)n,Tn是{an}前n项和,是否存在正数λ,对任意正整数n,k,使Tn-λx
<λ2恒成立?若存在,求λ的取值范围;若不存在,说明理由.
(1)求{xn}的通项公式;
(2)判别方程sin2xn+xncosxn+1=Sn是否有解,说明理由.
(3)设an=(
| 1 |
| 3 |
2 k |
考点:数列与不等式的综合,等差数列的性质
专题:计算题,等差数列与等比数列,三角函数的求值,不等式的解法及应用
分析:(1)运用等差数列的通项公式和求和公式,解方程,即可得到首项和公差,进而得到通项公式;
(2)化简整理,得到sin2(2n-1)+(2n-1)cos(2n-1)+1=n2,对n讨论,①n=1时,②n=2时,③n≥3时,解方程,结合正弦函数和余弦函数的值域,即可判断;
(3)方法一、通过等比数列的求和公式,运用恒成立思想,求出不等式左边的最大值,即可得到;
方法二、运用参数分离,结合等比数列的求和公式,数列的单调性,即可得到不等式解得即可.
(2)化简整理,得到sin2(2n-1)+(2n-1)cos(2n-1)+1=n2,对n讨论,①n=1时,②n=2时,③n≥3时,解方程,结合正弦函数和余弦函数的值域,即可判断;
(3)方法一、通过等比数列的求和公式,运用恒成立思想,求出不等式左边的最大值,即可得到;
方法二、运用参数分离,结合等比数列的求和公式,数列的单调性,即可得到不等式解得即可.
解答:
解:(1)由x3=5,S5+x5=34,
所以
解得
,
即有xn=2n-1;
(2)由于sin2xn+xncosxn+1=Sn,由于xn=2n-1,
Sn=
(1+2n-1)n=n2,
则方程为:sin2(2n-1)+(2n-1)cos(2n-1)+1=n2,
①n=1时,sin21+cos1=0无解;
②n=2时,sin23+3cos3+1=4所以cos23-3cos3+2=0
所以cos3=1,cos3=2,无解;
③n≥3时,sin2(2n-1)+(2n-1)cos(2n-1)+1<1+(2n-1)+1=2n+1<n2,
所以sin2(2n-1)+(2n-1)cos(2n-1)+1=n2,无解.
综上所述,对于一切正整数原方程都无解;
(3)解法一:an=(
)n,则Tn=
=
[1-(
)n],
又Tn-λx
<λ2恒成立,Tn>0,λ>0,
所以当Tn取最大值,xk2取最小值时,Tn-λx
取到最大值.
又Tn<
,xk2=(2k-1)2≥1,所以
-λ≤λ2
即λ2+λ-
≥0 故λ≥
;
解法二:由Tn-λx
<λ2恒成立,则
[1-(
)n]-λ(2k-1)2<λ2恒成立.
即λ2+λ(2k-1)2>
[1-(
)n]max,λ2+λ(2k-1)2≥
,又λ>0,
所以(2k-1)2≥
,[(2k-1)]max≥
,
所以1≥
,
即λ2+λ-
≥0 故λ≥
.
所以
|
|
即有xn=2n-1;
(2)由于sin2xn+xncosxn+1=Sn,由于xn=2n-1,
Sn=
| 1 |
| 2 |
则方程为:sin2(2n-1)+(2n-1)cos(2n-1)+1=n2,
①n=1时,sin21+cos1=0无解;
②n=2时,sin23+3cos3+1=4所以cos23-3cos3+2=0
所以cos3=1,cos3=2,无解;
③n≥3时,sin2(2n-1)+(2n-1)cos(2n-1)+1<1+(2n-1)+1=2n+1<n2,
所以sin2(2n-1)+(2n-1)cos(2n-1)+1=n2,无解.
综上所述,对于一切正整数原方程都无解;
(3)解法一:an=(
| 1 |
| 3 |
| ||||
1-
|
| 1 |
| 2 |
| 1 |
| 3 |
又Tn-λx
2 k |
所以当Tn取最大值,xk2取最小值时,Tn-λx
2 k |
又Tn<
| 1 |
| 2 |
| 1 |
| 2 |
即λ2+λ-
| 1 |
| 2 |
| ||
| 2 |
解法二:由Tn-λx
2 k |
| 1 |
| 2 |
| 1 |
| 3 |
即λ2+λ(2k-1)2>
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
所以(2k-1)2≥
| ||
| λ |
| ||
| λ |
所以1≥
| ||
| λ |
即λ2+λ-
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查等差和等比数列的通项公式和求和公式,考查三角函数值的求解,考查参数分离和不等式恒成立问题转化为最值问题,考查运算能力,和判断能力,属于中档题和易错题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
已知P为曲线y=lnx上一点,则点P到直线y=x距离最小值为( )
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、2 |
已知向量
、
满足
=
+2
,
=-5
+6
,
=7
-2
,则一定共线的三点是( )
| a |
| b |
| AB |
| a |
| b |
| BC |
| a |
| b |
| CD |
| a |
| b |
| A、A、B、D |
| B、A、B、C |
| C、B、C、D |
| D、A、C、D |
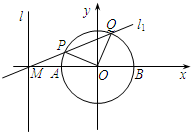 已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点(如图).
已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点(如图).