题目内容
椭圆
+
=1上的点M到左焦点F1的距离是2,N是MF1的中点,O为坐标原点,则|ON|为( )
| x2 |
| 25 |
| y2 |
| 9 |
| A、4 | ||
| B、2 | ||
| C、8 | ||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先作出椭圆的焦点△MF1F2,则ON为△MF1F2的中位线,易知,|ON|=
|MF2|,再由椭圆定义及MF1的长度得|MF2|,从而得|ON|的值.
| 1 |
| 2 |
解答:
解:设椭圆的右焦点为F2,连结MF2,ON,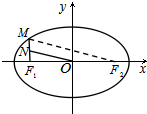 如右图所示.
如右图所示.
由椭圆方程
+
=1,得a=5,
由椭圆定义,得|MF1|+|MF2|=2a=2×5=10,
又|MF1|=2,∴|MF2|=10-2=8,
∵N为MF1的中点,O为F1F2的中点,
∴在△MF1F2中,有|ON|=
|MF2|=
×8=4.
故选A.
 如右图所示.
如右图所示.由椭圆方程
| x2 |
| 25 |
| y2 |
| 9 |
由椭圆定义,得|MF1|+|MF2|=2a=2×5=10,
又|MF1|=2,∴|MF2|=10-2=8,
∵N为MF1的中点,O为F1F2的中点,
∴在△MF1F2中,有|ON|=
| 1 |
| 2 |
| 1 |
| 2 |
故选A.
点评:本题考查了椭圆的定义,关键是充分挖掘图形的几何特征,将ON的长度转化为焦点三角形的边长问题来解决.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知方程x2+y2-2x-4y+m=0.
(1)若此方程表示圆,求实数m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M,N两点,且坐标原点O在以MN为直径的圆的外部,求实数m的取值范围.
(1)若此方程表示圆,求实数m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M,N两点,且坐标原点O在以MN为直径的圆的外部,求实数m的取值范围.
在平面直角坐标系中定义两点P(x1,y1),Q(x2,y2)之间的交通距离为d(P,Q)=|x1-x2|+|y1-y2|.若C(x,y)到点A(1,3),B(6,9)的交通距离相等,其中实数x,y满足0≤x≤10,0≤y≤10,则所有满足条件的点C的轨迹的长之和为( )
| A、1 | ||
B、5
| ||
| C、4 | ||
D、5(
|
下列说法中,错误的是( )
| A、有时可以把分类变量的不同取值用数字表示,但这时的数字除了分类以外没有其他含义 |
| B、在统计学中,独立性检验就是检验两个分类变量是否有关系的一种方法 |
| C、在进行独立性检验时,可以先利用二维条形图粗略的判断两个分类变量是否有关系 |
| D、通过二维条形图可以精确的给出所得结论的可靠程度 |
a、b是不互相垂直的异面直线,α、β是分别过a、b的平面,则下列四种情况:
①α∥β;②α⊥β;③a∥β;④a⊥β,
其中可能出现的有( )
①α∥β;②α⊥β;③a∥β;④a⊥β,
其中可能出现的有( )
| A、1种 | B、2种 | C、3种 | D、4种 |
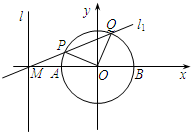 已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点(如图).
已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点(如图).