题目内容
若a∈R，则方程x2+4y2sina=1所表示的曲线一定不是（ ）
| A、直线 | B、圆 | C、抛物线 | D、双曲线 |
考点：轨迹方程
专题：圆锥曲线的定义、性质与方程
分析：对sinθ的取值进行讨论，由曲线方程的特性可判断方程x2+4y2sinθ=1所表示的曲线．
解答：
解：由题意得，方程x2+4y2sina=1，且-1≤sina≤1
当sinα=
时，曲线表示圆；
当sinα＜0时，曲线表示双曲线；
当sinα=0时，曲线表示直线；
当sinα＞0且sinα≠
时时，曲线表示椭圆，
而α是任意实数，方程x2+4y2sinα=1，都不含有y的一次项，曲线不表示抛物线．
故选：C．
当sinα=
| 1 |
| 4 |
当sinα＜0时，曲线表示双曲线；
当sinα=0时，曲线表示直线；
当sinα＞0且sinα≠
| 1 |
| 4 |
而α是任意实数，方程x2+4y2sinα=1，都不含有y的一次项，曲线不表示抛物线．
故选：C．
点评：本题考查方程与曲线，考查分类讨论的数学思想，熟练掌握与理解曲线标准方程的特征是关键．
练习册系列答案
相关题目
在等差数列{an}中，设公差d=1，a2是a1与a4的等比中项，则a1=（ ）
| A、2 | B、1 | C、2或1 | D、1或-1 |
已知向量
、
满足
=
+2
，
=-5
+6
，
=7
-2
，则一定共线的三点是（ ）
| a |
| b |
| AB |
| a |
| b |
| BC |
| a |
| b |
| CD |
| a |
| b |
| A、A、B、D |
| B、A、B、C |
| C、B、C、D |
| D、A、C、D |
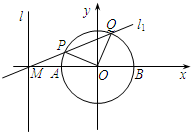已知直线l的方程为x=-2，且直线l与x轴交于点M，圆O：x2+y2=1与x轴交于A，B两点（如图）．