题目内容
设F1,F2是双曲线
-y2=1的两个焦点,点P在双曲线上,且
•
=0,则|
|•|
|的值等于 .
| x2 |
| 4 |
| PF1 |
| PF2 |
| PF1 |
| PF2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:运用双曲线的定义,以及向量的垂直的条件,以及勾股定理及运用,即可得到所求值.
解答:
解:双曲线
-y2=1的a=2,b=1,c=
,
则||
|-|
||=2a=4,|F1F2|=2c=2
,
由于
•
=0,则
⊥
,
则有|
2|+||
|2=|
|2,
即有||PF1|-|PF2||2+2|
|•|
|=|
|2,
即42+2|
|•|
|=20,
则|
|•|
|=2.
故答案为:2.
| x2 |
| 4 |
| 5 |
则||
| PF1 |
| PF2 |
| 5 |
由于
| PF1 |
| PF2 |
| PF1 |
| PF2 |
则有|
| PF1 |
| PF2 |
| F1F2 |
即有||PF1|-|PF2||2+2|
| PF1 |
| PF2 |
| F1F2 |
即42+2|
| PF1 |
| PF2 |
则|
| PF1 |
| PF2 |
故答案为:2.
点评:本题考查双曲线的定义和方程、性质,考查平面向量的数量积的性质,考查运算能力,属于中档题.

练习册系列答案
相关题目
方程(1+i)x2+(1+5i)x-(2-6i)=0有实根,则这个实根的值是( )
| A、2 | B、1 | C、-2 | D、-1 |
已知方程x2+y2-2x-4y+m=0.
(1)若此方程表示圆,求实数m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M,N两点,且坐标原点O在以MN为直径的圆的外部,求实数m的取值范围.
(1)若此方程表示圆,求实数m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M,N两点,且坐标原点O在以MN为直径的圆的外部,求实数m的取值范围.
已知P为曲线y=lnx上一点,则点P到直线y=x距离最小值为( )
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、2 |
正四面体棱长为1,其外接球的表面积为( )
A、
| ||
| B、π | ||
C、
| ||
| D、3π |
下列说法中,错误的是( )
| A、有时可以把分类变量的不同取值用数字表示,但这时的数字除了分类以外没有其他含义 |
| B、在统计学中,独立性检验就是检验两个分类变量是否有关系的一种方法 |
| C、在进行独立性检验时,可以先利用二维条形图粗略的判断两个分类变量是否有关系 |
| D、通过二维条形图可以精确的给出所得结论的可靠程度 |
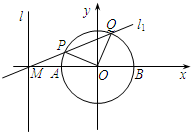 已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点(如图).
已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点(如图).