��Ŀ����
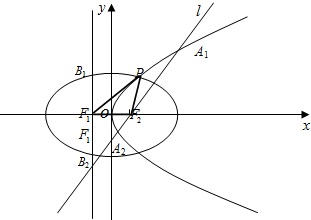 ��ͼ����������C1��y2=4mx��m��0��������x�ύ��F1������ΪF2����F1��F2Ϊ���㣬������e=
��ͼ����������C1��y2=4mx��m��0��������x�ύ��F1������ΪF2����F1��F2Ϊ���㣬������e=| 1 |
| 2 |
����m=1ʱ������Բ�ķ��̼������ߵķ��̣�
�����ڣ��������£�������F2��ֱ��l��������C1����A1��A2��������߶�A1A2Ϊֱ����Բ�����ж�������C1��������ԲC2�Ľ���B1��B2��Բ��λ�ù�ϵ��
�����Ƿ����ʵ��m��ʹ�á�PF1F2�ı߳�����������Ȼ���������ڣ����������ʵ��m���������ڣ���˵�����ɣ�
���㣺ֱ����Բ���ߵ��ۺ�����
ר�⣺������,Բ�����е���ֵ�뷶Χ����
����������m=1ʱ����֪c=1��a=2��b=
���Ӷ�����Բ���̼��߷��̣�
������������ֱ��l�ķ���Ϊ��x=ky+1��k��R����y2=4x�����ɵ�y2-4ky-4=0������ȡB1 (-1��
)�������
•
��0���ʵ�B1��Բ�ϻ�Բ�⣬�ʵ�B1��B2��Բ�ϻ�Բ�⣻
�������������������ʵ��m��ͨ���ڶ������֪������PF1F2�ı߳��ֱ���
m ��
m ��
m���Ӷ����m���ɣ�
| 3 |
������������ֱ��l�ķ���Ϊ��x=ky+1��k��R����y2=4x�����ɵ�y2-4ky-4=0������ȡB1 (-1��
| 3 |
| 2 |
| B1A1 |
| B1A2 |
�������������������ʵ��m��ͨ���ڶ������֪������PF1F2�ı߳��ֱ���
| 5 |
| 3 |
| 6 |
| 3 |
| 7 |
| 3 |
���
�⣺����m=1ʱ��F1��-1��0����F2��1��0����
��c=1������������e=
֪��
a=2����b=
��
����Բ����Ϊ
+
=1��
���߷���Ϊx=
=4��
������������ֱ��l�ķ���Ϊ��x=ky+1��k��R��
��x=ky+1����y2=4x�ã�
y2-4ky-4=0��
��A1��x1��y1����A2��x2��y2����
��Τ�ﶨ����y1+y2=4k��y1y2=-4��
����Բ�������ߵĶԳ��ԣ�ֻҪ�ж�B1��B2��һ�㼴�ɣ�
����ȡB1 (-1��
)��
��
=(x1+1��y1-
)��
=(x2+1��y2-
)��
��
•
=��x1+1����x2+1��+��y1-
����y2-
��
=x1x2+��x1+x2��+1+y1y2-
��y1+y2��+
=4k2-6k+
=4��k-
��2��
��Ϊk��R������
•
��0��
����B1��Բ�ϻ�Բ�⣬�ʵ�B1��B2��Բ�ϻ�Բ�⣮
�������������������ʵ��m��
��������c=m��a=2m��|F1F2|=2m��
����|PF1|=r1��|PF2|=r2��
��r1+r2=2a=4m��
��P��x0��y0����
����������C1��r2=x0+m��
������ԲC2��
=e=
��
��r2=
(4m-x0)��
��x0+m=
(4m-x0)��ã�x0=
m��
��r2=
m���Ӷ� r1=
m��
��ˣ�������PF1F2�ı߳��ֱ���
m ��
m ��
m��
����m=3ʱ����ʹ������PF1F2�ı߳�����������Ȼ����
��c=1������������e=
| 1 |
| 2 |
a=2����b=
| 3 |
����Բ����Ϊ
| x2 |
| 4 |
| y2 |
| 3 |
���߷���Ϊx=
| a2 |
| c |
������������ֱ��l�ķ���Ϊ��x=ky+1��k��R��
��x=ky+1����y2=4x�ã�
y2-4ky-4=0��
��A1��x1��y1����A2��x2��y2����
��Τ�ﶨ����y1+y2=4k��y1y2=-4��
����Բ�������ߵĶԳ��ԣ�ֻҪ�ж�B1��B2��һ�㼴�ɣ�
����ȡB1 (-1��
| 3 |
| 2 |
��
| B1A1 |
| 3 |
| 2 |
| B1A2 |
| 3 |
| 2 |
��
| B1A1 |
| B1A2 |
| 3 |
| 2 |
| 3 |
| 2 |
=x1x2+��x1+x2��+1+y1y2-
| 3 |
| 2 |
| 9 |
| 4 |
=4k2-6k+
| 9 |
| 4 |
| 3 |
| 4 |
��Ϊk��R������
| B1A1 |
| B1A2 |
����B1��Բ�ϻ�Բ�⣬�ʵ�B1��B2��Բ�ϻ�Բ�⣮
�������������������ʵ��m��
��������c=m��a=2m��|F1F2|=2m��
����|PF1|=r1��|PF2|=r2��
��r1+r2=2a=4m��
��P��x0��y0����
����������C1��r2=x0+m��
������ԲC2��
| r2 | ||
|
| 1 |
| 2 |
��r2=
| 1 |
| 2 |
��x0+m=
| 1 |
| 2 |
| 2 |
| 3 |
��r2=
| 5 |
| 3 |
| 7 |
| 3 |
��ˣ�������PF1F2�ı߳��ֱ���
| 5 |
| 3 |
| 6 |
| 3 |
| 7 |
| 3 |
����m=3ʱ����ʹ������PF1F2�ı߳�����������Ȼ����
���������⿼����Բ���ߵ�λ�ù�ϵ��Ӧ�ã�Ӧ�õ���Τ�ﶨ������������������ѣ��������⣮

��ϰ��ϵ�д�
 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
�����Ŀ
���������ⳤΪ1���������ı����Ϊ��������
A��
| ||
| B���� | ||
C��
| ||
| D��3�� |
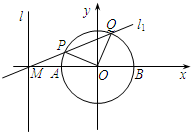 ��ֱ֪��l�ķ���Ϊx=-2����ֱ��l��x�ύ�ڵ�M��ԲO��x2+y2=1��x�ύ��A��B���㣨��ͼ����
��ֱ֪��l�ķ���Ϊx=-2����ֱ��l��x�ύ�ڵ�M��ԲO��x2+y2=1��x�ύ��A��B���㣨��ͼ����