题目内容
19.已知向量$\overrightarrow{a}$=(-x,2),$\overrightarrow{b}$=(x,x-2),则$\overrightarrow{a}$•$\overrightarrow{b}$的最大值是-3.分析 直接写出数量积的坐标表示,然后利用配方法求最值.
解答 解:∵$\overrightarrow{a}$=(-x,2),$\overrightarrow{b}$=(x,x-2),
则$\overrightarrow{a}$•$\overrightarrow{b}$=-x2+2(x-2)=-x2+2x-4=-(x2-2x+1)-3
=-(x-1)2-3≤-3.
∴$\overrightarrow{a}$•$\overrightarrow{b}$的最大值是-3.
故答案为:-3.
点评 本题考查了平面向量数量积的坐标运算,考查了利用配方法求二次函数的最值,是基础的计算题.

练习册系列答案
相关题目
9.已知直线l经过点A(4,1),B(6,3),则直线l的倾斜角是( )
| A. | 0° | B. | 30° | C. | 45° | D. | 60° |
11.若复数z满足(1-2i)z=2+i,则z的共轭复数是( )
| A. | -$\frac{3}{5}$i | B. | $\frac{3}{5}$i | C. | i | D. | -i |
9.记方程①:x2+a1x+1=0,方程②:x2+a2x+2=0,方程③:x2+a3x+4=0,其中a1,a2,a3是正实数.当a1,a2,a3成等比数列时,下列选项中,能推出方程③无实根的是( )
| A. | 方程①有实根,且②有实根 | B. | 方程①有实根,且②无实根 | ||
| C. | 方程①无实根,且②有实根 | D. | 方程①无实根,且②无实根 |
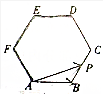 如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=k,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$,0]∪[k,$\frac{3}{2}{k}^{2}$].
如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=k,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$,0]∪[k,$\frac{3}{2}{k}^{2}$].