题目内容
11．
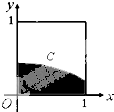在如图所示的正方形中随机取一点，则此点落入阴影部分（曲线C是函数f（x）=$\frac{1}{\sqrt{2π}}$${\;}^{{e}^{-\frac{{x}^{2}}{2}}}$ 的图象）的概率为（ ）注：P（μ-σ＜x≤μ+σ）=0.6826，P（μ-2σ＜x≤μ+2σ）=0.9544，P（μ-3σ＜x≤μ+3σ）=0.9974．
| A． | 0.2386 | B． | 0.2718 | C． | 0.3413 | D． | 0.4772 |
分析 曲线C是函数f（x）=$\frac{1}{\sqrt{2π}}$${\;}^{{e}^{-\frac{{x}^{2}}{2}}}$ 的图象，可得μ=0，σ=1，求出P（0＜X≤1）=$\frac{1}{2}$×0.6826=0.3413，即可得出结论．
解答 解：由题意，曲线C是函数f（x）=$\frac{1}{\sqrt{2π}}$${\;}^{{e}^{-\frac{{x}^{2}}{2}}}$ 的图象，
∴μ=0，σ=1，
P（0＜X≤1）=$\frac{1}{2}$×P（-1＜X≤1）=$\frac{1}{2}$×0.6826=0.3413，
故选：C．
点评 本题考查正态分布曲线的特点及曲线所表示的意义，考查正态分布中两个量μ和σ的应用，考查曲线的对称性，属于基础题．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
16．掷两颗均匀的骰子，则点数之和为7的概率等于（ ）
| A． | $\frac{1}{18}$ | B． | $\frac{1}{9}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{2}$ |
4．某程序框图如图所示，若该程序运行后输出的S的值为72，则判断框内应填入的条件可以是（ ）
| A． | n≤8？ | B． | n≤9？ | C． | n≤10？ | D． | n≤11？ |
1．设等差数列{an}满足：$\frac{{{{sin}^2}{a_2}-{{cos}^2}{a_2}+{{cos}^2}{a_2}{{cos}^2}{a_7}-{{sin}^2}{a_2}{{sin}^2}{a_7}}}{{sin（{a_4}+{a_5}）}}=1$，公差$d∈（-\frac{1}{2}，0）$若当且仅当n=11时，数列{an}的前n项和Sn取得最大值，则首项a1的取值范围是（ ）
| A． | $（\frac{10}{11}π，π）$ | B． | $[\frac{10}{11}π，π）$ | C． | $[π，\frac{11}{10}π）$ | D． | $（π，\frac{11}{10}π）$ |