题目内容
19．已知向量$\overrightarrow a=（2m，4），\overrightarrow b=（m-1，-1）$，若$\overrightarrow a⊥\overrightarrow b$，则实数m的值为2或-1．分析 由$\overrightarrow a⊥\overrightarrow b$，可得$\overrightarrow{a}•\overrightarrow{b}$=0，解出即可．
解答 解：∵$\overrightarrow a⊥\overrightarrow b$，
∴$\overrightarrow{a}•\overrightarrow{b}$=2m（m-1）-4=0，
化为m2-m-2=0，
解得m=2或-1．
故答案为：2或-1．
点评 本题考查了向量垂直与数量积的关系，属于基础题．
练习册系列答案
相关题目
9．已知△ABC中，∠A=$\frac{π}{6}$，AB=3$\sqrt{3}$，AC=3，在线段BC上任取一点P，则线段PB的长大于2的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{5}$ |
10．一袋中有5个白球、3个红球，现从袋中往外取球，每次任取一个记下颜色后放回，直到红球出现10次时停止，设停止时共取了X次球，则P（X=12）等于（ ）
| A． | C${\;}_{12}^{10}$（$\frac{3}{8}$）10（$\frac{5}{8}$）2 | B． | C${\;}_{12}^{9}$（$\frac{3}{8}$）9（$\frac{5}{8}$）2（$\frac{3}{8}$） | C． | C${\;}_{11}^{9}$（$\frac{5}{8}$）9（$\frac{3}{8}$）2 | D． | C${\;}_{11}^{9}$（$\frac{3}{8}$）10（$\frac{5}{8}$）2 |
7．已知f（x）=$\left\{\begin{array}{l}{x，x≥0}\\{1，x＜0}\end{array}\right.$．则不等式f（x2）＞f（3-2x）的解集为（ ）
| A． | （-∞，-1）∪（1，+∞） | B． | （-∞，-3）∪（1，+∞） | C． | （-∞，-3）∪（$\frac{1}{2}$，+∞） | D． | （-∞，-1）∪（$\frac{1}{2}$，+∞） |
14．若P（2，1）为圆（x-1）2+y2=36的弦AB的中点，则直线AB的方程是（ ）
| A． | x-y-3=0 | B． | 2x+y-3=0 | C． | x+y-1=0 | D． | x+y-3=0 |
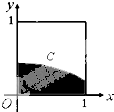在如图所示的正方形中随机取一点，则此点落入阴影部分（曲线C是函数f（x）=$\frac{1}{\sqrt{2π}}$${\;}^{{e}^{-\frac{{x}^{2}}{2}}}$ 的图象）的概率为（ ）