题目内容
2.在极坐标系中,圆A的方程为ρ=4cosθ,曲线C的参数方程为$\left\{\begin{array}{l}{x=1-2t}\\{y=-1+t}\end{array}\right.$(t为参数),则圆A的圆心到曲线C的距离是$\frac{3\sqrt{5}}{5}$.分析 已知直线C的参数方程为$\left\{\begin{array}{l}{x=1-2t}\\{y=-1+t}\end{array}\right.$(t为参数),将直线C先化为一般方程坐标,将圆C的极坐标方程化成直角坐标方程,然后再计算圆心A到直线C的距离.
解答 解:直线C的普通方程为x+2y+1=0,圆A的直角坐标方程为(x-2)2+y2=9,圆心是(2,0).
所以圆心A(2,0)到直线C的距离d=$\frac{|1×2+2×0+1|}{\sqrt{{1}^{2}+{2}^{2}}}$=$\frac{3\sqrt{5}}{5}$.
故答案是:$\frac{3\sqrt{5}}{5}$.
点评 此题考查参数方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解,这也是每年高考必考的热点问题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
11.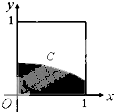 在如图所示的正方形中随机取一点,则此点落入阴影部分(曲线C是函数f(x)=$\frac{1}{\sqrt{2π}}$${\;}^{{e}^{-\frac{{x}^{2}}{2}}}$ 的图象)的概率为( )
在如图所示的正方形中随机取一点,则此点落入阴影部分(曲线C是函数f(x)=$\frac{1}{\sqrt{2π}}$${\;}^{{e}^{-\frac{{x}^{2}}{2}}}$ 的图象)的概率为( )
注:P(μ-σ<x≤μ+σ)=0.6826,P(μ-2σ<x≤μ+2σ)=0.9544,P(μ-3σ<x≤μ+3σ)=0.9974.
 在如图所示的正方形中随机取一点,则此点落入阴影部分(曲线C是函数f(x)=$\frac{1}{\sqrt{2π}}$${\;}^{{e}^{-\frac{{x}^{2}}{2}}}$ 的图象)的概率为( )
在如图所示的正方形中随机取一点,则此点落入阴影部分(曲线C是函数f(x)=$\frac{1}{\sqrt{2π}}$${\;}^{{e}^{-\frac{{x}^{2}}{2}}}$ 的图象)的概率为( )注:P(μ-σ<x≤μ+σ)=0.6826,P(μ-2σ<x≤μ+2σ)=0.9544,P(μ-3σ<x≤μ+3σ)=0.9974.
| A. | 0.2386 | B. | 0.2718 | C. | 0.3413 | D. | 0.4772 |