题目内容
【题目】若数列![]() 满足:存在正整数T,对于任意正整数n都有
满足:存在正整数T,对于任意正整数n都有![]() 成立,则称数列
成立,则称数列![]() 为周期数列,周期为T.已知数列
为周期数列,周期为T.已知数列![]() 满足
满足![]() ,
, ,则下列结论中错误的是( )
,则下列结论中错误的是( )
A.若![]() ,则m可以取3个不同的值;
,则m可以取3个不同的值;
B.若![]() ,则数列
,则数列![]() 是周期为3的数列;
是周期为3的数列;
C.对于任意的![]() 且T≥2,存在
且T≥2,存在![]() ,使得
,使得![]() 是周期为
是周期为![]() 的数列
的数列
D.存在![]() 且
且![]() ,使得数列
,使得数列![]() 是周期数列
是周期数列
【答案】D
【解析】
A. 若![]() ,根据
,根据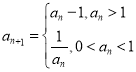 ,分别对
,分别对![]() 讨论求解即可; B.若
讨论求解即可; B.若![]() ,根据
,根据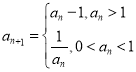 ,分别求得
,分别求得![]() 即可判断; C.通过B判断即可;D.用反证法判断.
即可判断; C.通过B判断即可;D.用反证法判断.
A.若![]() ,因为
,因为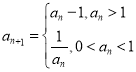 ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]() ,解得
,解得![]() ,不合题意,故m可以取3个不同的值,故正确;
,不合题意,故m可以取3个不同的值,故正确;
B.若![]() ,则
,则![]() ,所以
,所以![]() ,则数列
,则数列![]() 是周期为3的数列,故正确;
是周期为3的数列,故正确;
C.对于任意的![]() 且T≥2,存在
且T≥2,存在![]() ,使得
,使得![]() 是周期为
是周期为![]() 的数列,其否定为:.对于任意的
的数列,其否定为:.对于任意的![]() 且T≥2,不存在
且T≥2,不存在![]() ,使得
,使得![]() 是周期为
是周期为![]() 的数列,由B知原命题正确;
的数列,由B知原命题正确;
D.假设存在![]() 且
且![]() ,使得数列
,使得数列![]() 是周期数列,当
是周期数列,当![]() 时,
时,![]() ,此时,数列
,此时,数列![]() 不是周期数列,
不是周期数列,
当![]() 时,当
时,当![]() 时,
时,![]() ,
,![]() ,若
,若![]() ,
,![]() ,则
,则![]() ,即
,即![]() ,而
,而![]() 不为平方数,因此假设不正确,故数列
不为平方数,因此假设不正确,故数列![]() 不是周期数列,故错误.
不是周期数列,故错误.
故选:D

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目