题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)证明:当a=3时,函数![]() 有且只有两个零点.
有且只有两个零点.
【答案】(1)分类讨论,详见解析;(2)详见解析.
【解析】
(1)由![]() ,分
,分![]() 和
和![]() 两种情况进行讨论得出函数的单调性.
两种情况进行讨论得出函数的单调性.
(2)函数![]() 有且只有两个零点,即方程
有且只有两个零点,即方程![]() 有且只有两个实数根,即
有且只有两个实数根,即![]() 有且只有两个实数根,设
有且只有两个实数根,设![]() ,求出导数,求出函数
,求出导数,求出函数![]() 的单调区间,结合零点存在原理得出结论,使得问题得证.
的单调区间,结合零点存在原理得出结论,使得问题得证.
解:(1)![]() 的定义域为
的定义域为![]() ,
,![]() .
.
①![]() 时,
时,![]() ,则
,则![]() 在
在![]() 是单调递增;
是单调递增;
②![]() 时,由
时,由![]() 得
得![]() ,当
,当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
综上,![]() 时
时![]() 在
在![]() 是单调递增;
是单调递增;
![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2).![]()
![]()
![]() ,令
,令![]() ,
,
则![]() ,令
,令![]() ,
,
显然![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,
,![]()
易知存在唯一![]() ,使
,使![]() ,且
,且![]() 时,
时,![]() ,即
,即![]() ,
,![]() 单调递减;
单调递减;
![]() 时,
时,![]() ,即
,即![]() ,
,![]() 单调递增,
单调递增,
所以![]() 至多有两个零点.又
至多有两个零点.又![]()
![]() ,
,![]() ,
,![]() ,
,
故![]() 在区间
在区间![]() 和
和![]() 各有一个零点.所以函数
各有一个零点.所以函数![]() 有且只有两个零点.
有且只有两个零点.

练习册系列答案
相关题目
【题目】2016年入冬以来,各地雾霾天气频发,![]() 频频爆表(
频频爆表(![]() 是指直径小于或等于
是指直径小于或等于![]() 微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与![]() 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与![]() 的数据如下表:
的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
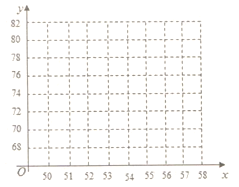
(1)请根据上述数据,在上面给出的坐标系中画出散点图;
(2)试判断![]() 与
与![]() 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,若没有,请说明理由;
,若没有,请说明理由;