题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过右焦点
,过右焦点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,
两点,![]() 的周长为
的周长为![]() ,点
,点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 、
、![]() 的斜率
的斜率![]() ,
,![]() ,请问
,请问![]() 是否为定值?若是定值,求出其定值;若不是,说明理由.
是否为定值?若是定值,求出其定值;若不是,说明理由.
【答案】(1)![]() (2)
(2)![]() 是定值,且为
是定值,且为![]()
【解析】
(1)由![]() 的周长为
的周长为![]() ,得到
,得到![]() ,即
,即![]() .再由离心率求得
.再由离心率求得![]() ,从而可得
,从而可得![]() ,得椭圆方程.
,得椭圆方程.
(2)直线l斜率不存在时,![]() ,直线
,直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,由直线方程与椭圆方程联立消元,可得
,由直线方程与椭圆方程联立消元,可得![]() ,计算
,计算![]() ,并代入
,并代入![]() 可得
可得![]() .这样就得出结论.
.这样就得出结论.
(1)由![]() 的周长为
的周长为![]() ,得到
,得到![]() ,即
,即![]() .
.
又因为![]() ,所以
,所以![]() ,
,
故![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 与
与![]() 轴不垂直时,
轴不垂直时,
设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,
把直线![]() 的方程代入
的方程代入![]() ,得
,得![]() ,
,
则![]() ,
,![]() ,
,
因为![]()
![]()
![]() ,
,
而![]() .
.
即![]() .
.
当直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() 是定值.
是定值.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案【题目】独立性检验中,假设![]() :运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得
:运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得![]() 的观测值
的观测值![]() .下列结论正确的是( )
.下列结论正确的是( )
附:
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
A. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动有关
B. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动无关
C. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动有关
D. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动无关
【题目】2016年入冬以来,各地雾霾天气频发,![]() 频频爆表(
频频爆表(![]() 是指直径小于或等于
是指直径小于或等于![]() 微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与![]() 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与![]() 的数据如下表:
的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
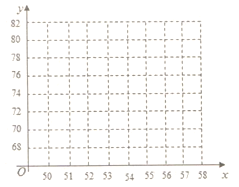
(1)请根据上述数据,在上面给出的坐标系中画出散点图;
(2)试判断![]() 与
与![]() 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,若没有,请说明理由;
,若没有,请说明理由;