题目内容
【题目】已知函数![]()
(1)讨论![]() 的极值点的个数;
的极值点的个数;
(2)若![]() 有两个极值点x1,x2(x1<x2),且
有两个极值点x1,x2(x1<x2),且![]() 求
求![]() 的最小值
的最小值
【答案】(1)见解析;(2)![]()
【解析】
(1)求导数得![]() ,当
,当![]() 通过讨论判别式
通过讨论判别式![]() 与0的关系,得函数单调性,由单调性即可得函数的极值问题;(2)
与0的关系,得函数单调性,由单调性即可得函数的极值问题;(2)![]() 有两个极值点
有两个极值点![]() 可知
可知![]() 为方程
为方程![]() 的两个根,用
的两个根,用![]() 表示出为
表示出为![]() ,令
,令![]() ,构造函数
,构造函数![]() 求导判单调性即可得到最值.
求导判单调性即可得到最值.
(1)法一:由题意得![]() ,
,
令![]() ,即
,即![]() 。.
。.
①当![]() ,即
,即![]() 时,
时,![]() 对任意
对任意![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立,此时
恒成立,此时![]() 没有极值点。
没有极值点。
②当![]() ,即
,即![]() 或
或![]() 时。
时。
若![]() ,设方程
,设方程![]() 的两个不同实根为
的两个不同实根为![]() ,不妨设
,不妨设![]() ,
,
则![]() ,
,
故![]() ,
,
![]() 当
当![]() 或
或![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
故![]() 是函数
是函数![]() 的两个极值点。
的两个极值点。
若![]() ,设方程
,设方程![]() 的两个不同实根为
的两个不同实根为![]() ,
,
则![]() ,故
,故![]() 。
。
![]() 当
当![]() 时,
时,![]() ,故函数
,故函数![]() 没有极值点。
没有极值点。
当![]() 时,函数
时,函数![]() 没有极值点。
没有极值点。
法二:![]() ,
,
![]() 。.
。.
①当![]() ,即
,即![]() 时,
时,![]() 对任意
对任意![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增,
上单调递增,![]() 没有极值点。.
没有极值点。.
②当![]() ,即
,即![]() 时,
时,![]() 有两个不等正实数解,设为
有两个不等正实数解,设为![]() ,
,
![]() 。
。
不妨设![]() ,则当
,则当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,
,![]() 单调递增,所以
单调递增,所以![]() 分别为
分别为![]() 的极大值点和极小值点。
的极大值点和极小值点。
故![]() 有两个极值点。.
有两个极值点。.
综上所述,当![]() 时,
时,![]() 没有极值点,
没有极值点,
当![]() 时,
时,![]() 有两个极值点。
有两个极值点。
(2)由题意知,![]() ,
,
则易知![]() 为方程
为方程![]() 的两个根,且
的两个根,且![]() ,
,
所以![]()
![]()
![]()
![]()
![]()
![]()
记![]() ,由
,由![]() 且
且![]() 知
知![]() ,
,
则![]() ,
,
记![]() ,
,
则![]() ,
,
故![]() 在
在![]() 上单调递减。
上单调递减。
由![]() 知
知![]() ,
,
从而![]() ,即
,即![]() ,
,
故![]() ,结合
,结合![]() ,解得
,解得![]() ,
,
从而![]() 的最小值为
的最小值为![]() ,
,
即![]() 的最小值为
的最小值为![]() 。
。

【题目】为了调查一款电视机的使用时间,研究人员对该款电视机进行了相应的测试,将得到的数据统计如下图所示:

并对不同年龄层的市民对这款电视机的购买意愿作出调查,得到的数据如下表所示:
愿意购买这款电视机 | 不愿意购买这款电视机 | 总计 | |
40岁以上 | 800 | 1000 | |
40岁以下 | 600 | ||
总计 | 1200 |
(1)根据图中的数据,试估计该款电视机的平均使用时间;
(2)根据表中数据,判断是否有99.9%的把握认为“愿意购买该款电视机”与“市民的年龄”有关;
(3)若按照电视机的使用时间进行分层抽样,从使用时间在![]() 和
和![]() 的电视机中抽取5台,再从这5台中随机抽取2台进行配件检测,求被抽取的2台电视机的使用时间都在
的电视机中抽取5台,再从这5台中随机抽取2台进行配件检测,求被抽取的2台电视机的使用时间都在![]() 内的概率.
内的概率.
附: | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】独立性检验中,假设![]() :运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得
:运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得![]() 的观测值
的观测值![]() .下列结论正确的是( )
.下列结论正确的是( )
附:
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
A. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动有关
B. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动无关
C. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动有关
D. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动无关
【题目】流行性感冒(简称流感)是流感病毒引起的急性呼吸道感染,是一种传染性强、传播速度快的疾病.其主要通过空气中的飞沫、人与人之间的接触或与被污染物品的接触传播.流感每年在世界各地均有传播,在我国北方通常呈冬春季流行,南方有冬春季和夏季两个流行高峰.儿童相对免疫力低,在幼儿园、学校等人员密集的地方更容易被传染.某幼儿园将去年春期该园患流感小朋友按照年龄与人数统计,得到如下数据:
年龄( |
|
|
|
|
|
患病人数( |
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)计算变量![]() 、
、![]() 的相关系数
的相关系数![]() (计算结果精确到
(计算结果精确到![]() ),并回答是否可以认为该幼儿园去年春期患流感人数与年龄负相关很强?(若
),并回答是否可以认为该幼儿园去年春期患流感人数与年龄负相关很强?(若![]() ,则
,则![]() 、
、![]() 相关性很强;若
相关性很强;若![]() ,则
,则![]() 、
、![]() 相关性一般;若
相关性一般;若![]() ,则
,则![]() 、
、![]() 相关性较弱.)
相关性较弱.)
参考数据:![]() .
.
参考公式: ,
,
相关系数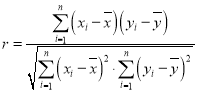 .
.