题目内容
已知数列{an}满足a1=2,an+1=
(n∈N*),则a1•a2•a3•…•a2008的值为 .
| 1+an |
| 1-an |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:由于数列{an}满足a1=2,an+1=
(n∈N*),可得a2=-3,a3=-
,a4=
,a5=2,…,因此an+4=an.即可得出.
| 1+an |
| 1-an |
| 1 |
| 2 |
| 1 |
| 3 |
解答:
解:∵数列{an}满足a1=2,an+1=
(n∈N*),
∴a2=-3,a3=-
,a4=
,a5=2,…,
∴an+4=an.
又a1a2a3a4=2×(-3)×(-
)×
=1.
则a1•a2•a3•…•a2008=(a1a2a3a4)502=1.
故答案为:1.
| 1+an |
| 1-an |
∴a2=-3,a3=-
| 1 |
| 2 |
| 1 |
| 3 |
∴an+4=an.
又a1a2a3a4=2×(-3)×(-
| 1 |
| 2 |
| 1 |
| 3 |
则a1•a2•a3•…•a2008=(a1a2a3a4)502=1.
故答案为:1.
点评:本题考查了数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
若0<x<
,0<y<
,且sinx=xcosy,则( )
| π |
| 2 |
| π |
| 2 |
A、y<
| ||||
B、
| ||||
C、
| ||||
| D、x<y |
表面积为4
的正四面体的各个顶点都在同一个球面上,则此球的体积为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图所示正方体AC1,下面结论错误的是( )
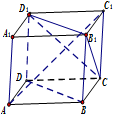

| A、BD∥平面CB1D1 |
| B、AC1⊥BD |
| C、AC1⊥平面CB1D1 |
| D、异面直线AD与CB1角为60° |
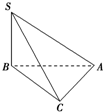 三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中:
三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,则以下结论中: